一、原函数不定积分的概念原函数的定义:

如果可导函数F(x)的导函数在区间I中是f & # 39(x)，即对于任意x∈I都有F & # 39(x)=f(x)或df(x)=f(x) dx，则函数F(x)称为F(x)(或f(x) dx)在区间I的原函数。

原函数存在定理；

如果函数f(x)在区间I中连续，那么在区间I中存在可导函数F(x)，使得每个x∈I都有F & # 39(x)=f(x)。

简单来说:

连续函数必有原函数。

不定积分的定义:

在区间I上，具有任意常数项的函数f(x)的原函数称为f(x)( f(x)dx)在区间I上的不定积分，记为∫ f(x)dx。符号∫称为整数，f(x)称为被积函数f(x)dx称为被积函数表达式，x

二、基本积分公式

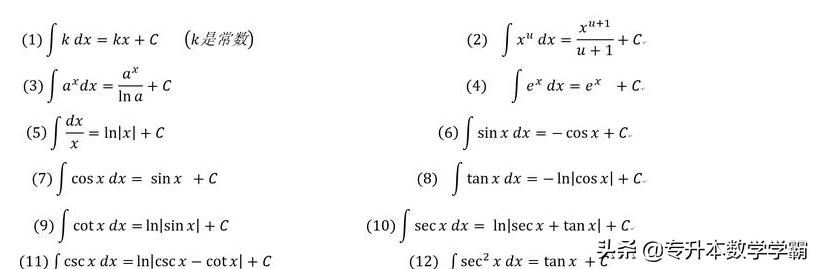
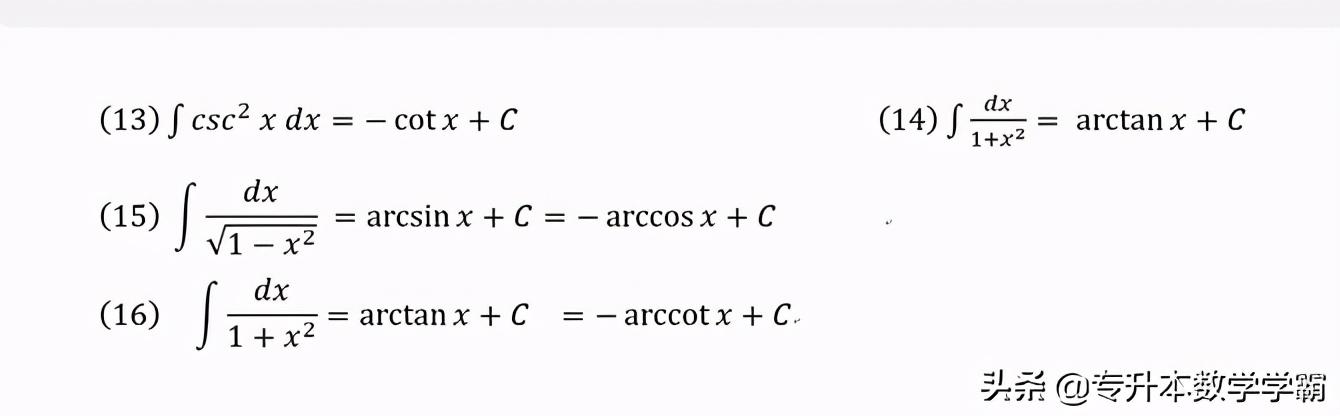
三、不定积分的性质

设函数f(x)和g(x)的原函数存在，则∫ [F (x) G (x)] dx = ∫ F (x) dx ∫ G (x) dx。注:封闭的加减积分可以分别加减。2.设函数f(x)和g(x)的原函数存在，k为非零常数，则

∫ k f(x) dx=k ∫ f(x) dx

记者:一个非零常数乘以一个积分的时候，你可以把常数拿出来，乘以不定积分。

第四，第一种替代积分法

如果f(u)有原函数，u=φ(x)可导，则有一个代入公式:

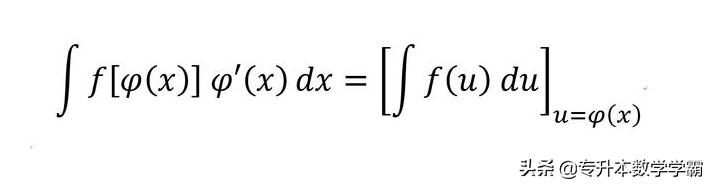
也被称为微分学。

第五，第二种代换积分法

设x=ψ(t)是单调可微函数，ψ& # 39；(t)≠0，而f[ψ(t)]ψ& # 39；(t)有原函数就有代换公式。

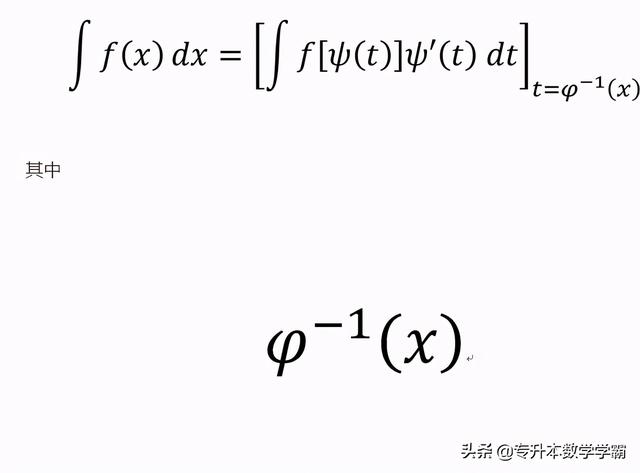
是x=ψ(x)的反函数。

三种常见的代换公式(注意:用三角形理解来记忆)

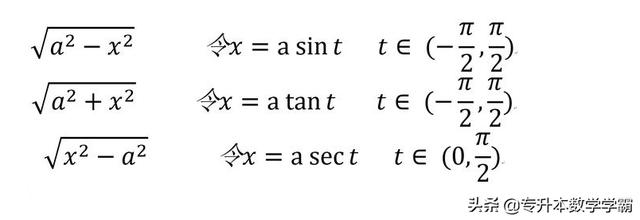
第二代换积分法求解的常见积分公式:

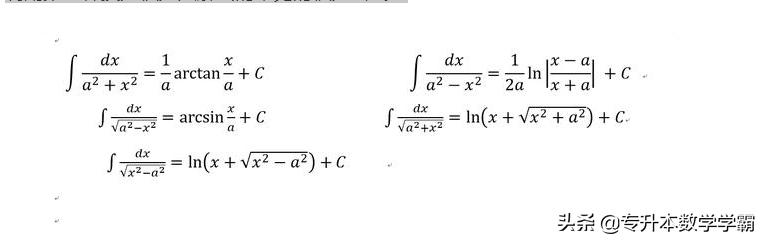
不及物动词部分积分法

设函数u=u(x)和v=v(x)有连续导数，则两个函数乘积的导数公式为(uv)& # 39；= u & # 39v+ uv & # 39；，移动该项，得到:u v & # 39=(u v)& # 39；-u & # 39；v

对这个方程的两边进行积分。

∫u v & # 39；dx = u v-∫u & # 39；V dx称为部分积分公式。

按零件的集成顺序集成:反对幂指三，指从后面集成容易，先集成那个。积分的顺序:先三角函数，再指数函数，再幂函数，再对数函数，最后反三角函数。

七、有理函数的积分

1.利用换元法:∫ f[ g(x) ]dx，设t=g(x)，可以发现x= u(t)，t=g(x)，x= u(t)是反函数，dx=u(t)dt是∫ f(。

2.有理函数的积分

两个多项式的商P(x)/Q(x)称为有理函数，也称为有理分式。

当分子多项式P(x)的次数小于分母多项式的次数时，这个有理函数叫做真分数。

当分子多项式P(x)的次数大于分母多项式的次数时，这个有理函数叫做假分数。

分母Q(x)可以分解成两个多项式的乘积。

Q(x)=Q(x1)Q(x2)与Q(x1)和Q(x2)没有公因数，可分为两个真分数之和。

p(x)/Q(x)= P1(x)/Q1(x)+P2(x)/Q2(x).

例如，有两个因素A和B满足

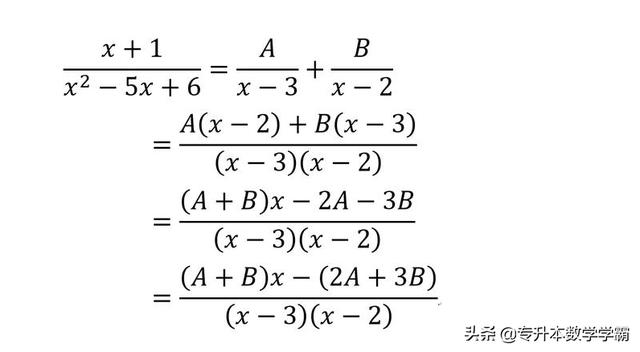
幂等系数，有

A+B=1，-(2A+3B)=1，

解决办法

A=4，B=-3

3.可以转化为有理函数的积分(复有理公式)

用代换积分法积分，使一个量等于复数公式，求解反函数公式得到积分。

以上内容纯属个人总结意见，不代表官方观点。以上内容是不定积分，不定积分的内容。考虑到这一点，我们下次继续讨论定积分的内容。最后，喜欢这个内容的朋友请喜欢。如果下次想看，请收藏！欢迎大家在评论区评论。请关注我，我会持续发布关于专科生数学考试的文章或视频。感谢您的支持！希望能帮你考上专科。最后祝大家梦想成真！