& gt模式识别讲座中CC BY 4.0下的图片。

这些是FAU的YouTube讲座“模式识别”的讲义。这是讲座视频和配套幻灯片的完整记录。幻灯片的来源可以在这里提供。我们希望你喜欢这个视频。抄本几乎完全由自动剥离机生成，只进行轻微的手工修改。如果发现错误，请告诉我们！

欢迎回到模式识别！今天，我们要复习一些对本课程剩余部分非常重要的基础知识。我们会考察简单分类，监督无监督学习，复习一点概率论。所以这是一种复习。如果你和概率论不再强大，你会在这个视频里找到我们非常有用的例子。

& gt模式识别讲座中CC BY 4.0下的图片。

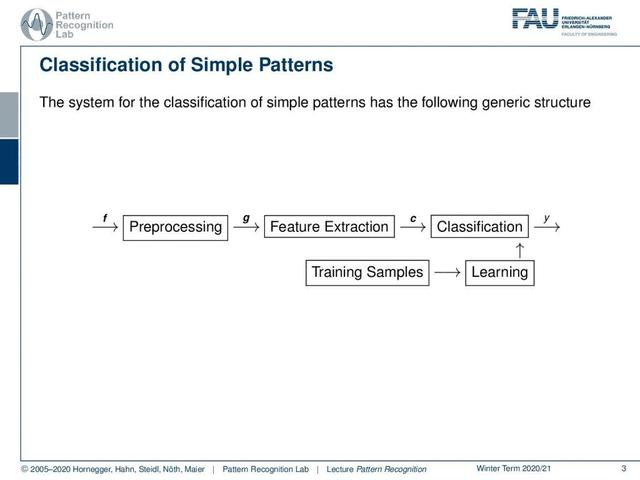
让我们进入模式识别的基础知识。因此，我们回顾了之前视频中的分类系统。我们有我们的模式识别系统，包括预处理，特征提取和分类。大家可以看到，我们通常用f来表示输入系统的信号。然后我们要用G作为预处理图像。特征提取之后，我们有一些抽象的特征C，然后用在分类中预测一些类y，当然这和我们用来学习问题参数的训练样本有关。

& gt模式识别讲座中CC BY 4.0下的图片。

通常，这些数据集由元组组成。所以我们有一些向量X‖，它们与一些类相关联，这里用y表示，这些元组可以形成一个训练数据集。现在使用这个数据集，我们可以估计所需分类系统的参数。所以，这是一个监督的案例。当然，还有一种无监督的情况，没有分类，但是你只需要观察x，x ^ 2等。所以你无法知道分类，但是你从观察到的样本中知道分布，所以你可以开始建模聚类等等。

& gt模式识别讲座中CC BY 4.0下的图片。

下面介绍一些符号。一般我们会在这里使用d维特征空中的向量x。向量通常与某个类别号相关联。因此您可以将其分配给{0，1}。所以这是一个2级问题，但是你也可以用-1和+1来表示类。暂且考察两类问题，但一般来说，也可以扩展到多层次问题。您可以在那里使用类别号，也可以使用热编码向量。在这种情况下，那么你的分类就不再是一个简单的数字或者标量，而是会被编码成一个向量。因此，如果你参加深入的研究，那么你会看到我们将在那里非常大量地使用这个概念。我们还需要什么？好吧，我们想谈谈概率。所以这里p(y)是某一类y的存在概率，这个基本上和问题的结构以及对应类的出现频率有关。我们将在接下来的几张幻灯片中研究一些示例。然后我们有一些证据通常是p(x)，所以这是观测到x的概率，这是一般情况，活在D维特征空。此外，还有一个联合概率。这基本上就是X和Y一起发生的概率。然后条件概率，特别是类条件概率，给定为给定y的x .然后就是所谓的后验概率对于给定的x是p .所以基本上，下面就是给你某一类的可能性的概率，给一些观测x .现在，这个就比较抽象了。我们来研究一些概率是如何构造的例子！

& gt模式识别讲座中CC BY 4.0下的图片。

我们会用一个很简单的例子，就是抛硬币。在抛硬币中，你基本上可以有两种结果，即头和尾。所以在这里，我们不是生活在D维特征空空间。相反，我们只有两个不同的离散观测值，我们是我们的观测结果x，这里可以看到，我们做了一个抛硬币的动作。我们有18个头，33条尾巴。总共有51个观察值和这些离散的观察值，我们现在可以尝试估计概率。所以这种情况下观察到前方的概率大概是35%。同理，我也可以算出相反的概率，大概是65%。现在，你看，我们只有证据，没有分类。让我们发出更复杂的问题。假设你是色盲，分不清颜色类别。所以这基本上是我们面临的问题。我们无法访问类别，但有一些真实的类别以某种方式隐藏起来。

& gt模式识别讲座中CC BY 4.0下的图片。

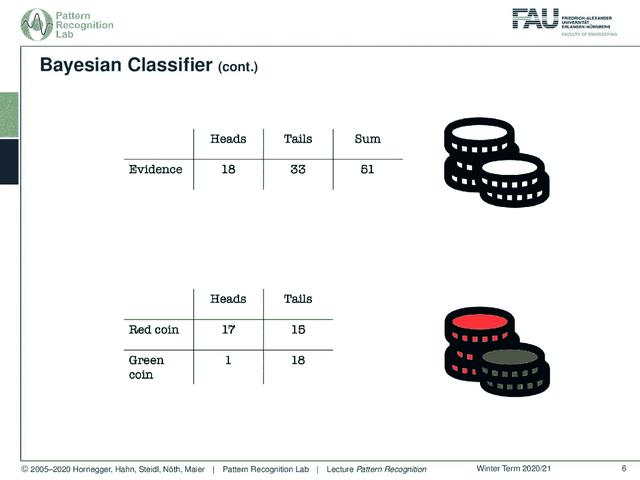
你可以想象我实际上有两种不同的硬币。所以我有一枚红色硬币和一枚绿色硬币。现在红币是出17头15尾，而我们绿币只出1尾18尾。所以绿色的硬币向对面倾斜。当然，我们也可以计算我们的行的总和，这将为我们提供这些数字。当然，我们也可以计算列的和。在这里，你已经看到，在最后一行，我们基本上有相同的证据，我们看到在顶部的表格。

& gt模式识别讲座中CC BY 4.0下的图片。

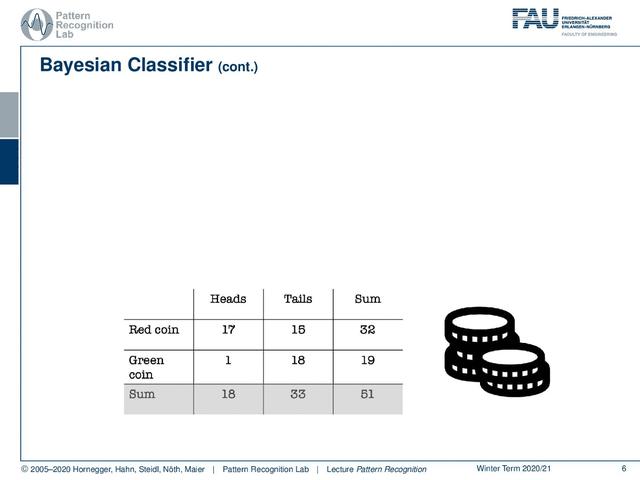
您现在可以查看最后一行。这基本就是我们色盲的情况。我们分不清两个硬币的区别，我们会有完全相同的概率:观察35%的正面和65%的反面。

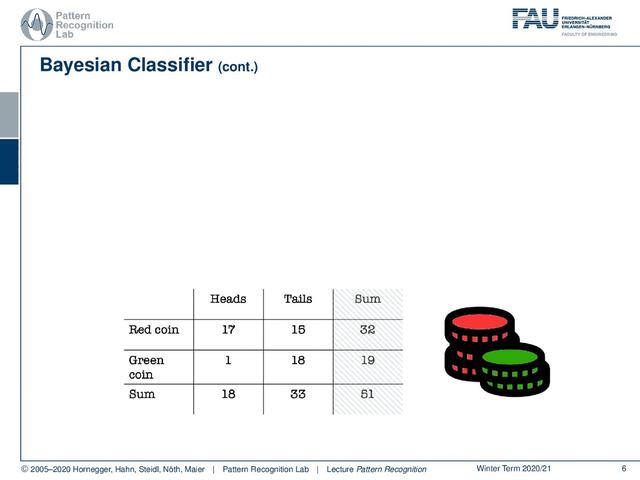
& gt模式识别讲座中CC BY 4.0下的图片。

我们还能做什么？当然我们也可以看看最后一栏。在这里，你可以看到我们本质上的分类前锋。使用红币的概率约为63%，使用绿币的概率为37%。所以如果有人在用这两个硬币，你可以反驳，然后他试图用这个有偏见的硬币。不是所有情况下都这样，只是这个人是偶尔在混这个币，因为可能你不想被骗。所以你只要把它混合起来，比如说37个项目，因为，当然，你想再赢一次。在其他情况下，你不想被抓住，所以这就是为什么你使用其他硬币。完美的感觉，对吧？所以让我们稍微研究一下联合概率。

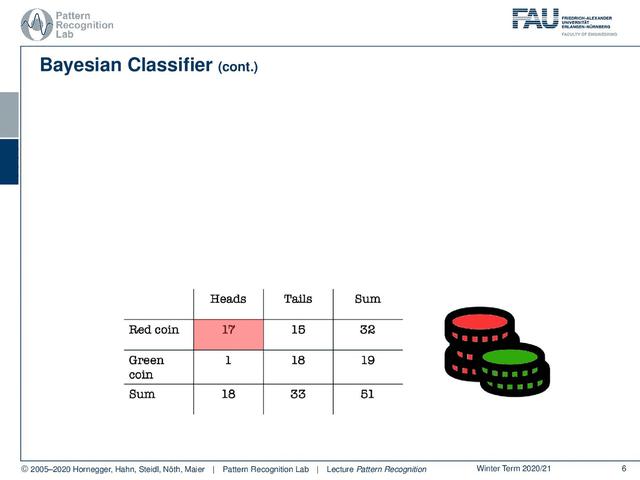
& gt模式识别讲座中CC BY 4.0下的图片。

现在，这将是你能同时观察到正面和红色硬币的概率。在这里，你可以看到这是17次，总共51次观测。所以这相当于33%左右的概率。当然，我们也可以用反币和绿币做类似的东西，会相当于35%左右。现在，如果我们想计算这些数字，我们需要访问类分布。所以我们需要知道哪些硬币是可用的，我们也需要知道实际的观察和我们的证据是什么。现在，我们还可以用这个美丽的形式做什么呢？

& gt模式识别讲座中CC BY 4.0下的图片。

我们当然可以分析我们的硬币。这里你认为我们的绿币偏向反面，你可以根据绿币计算正概率。所以，如果我开始搞乱这个，我只会有5%的几率产生积极的一面，95%的几率产生消极的一面。这基本上是我没有的信息。我收到了一些信息，我得到了正面和负面的观察，因为我是色盲。

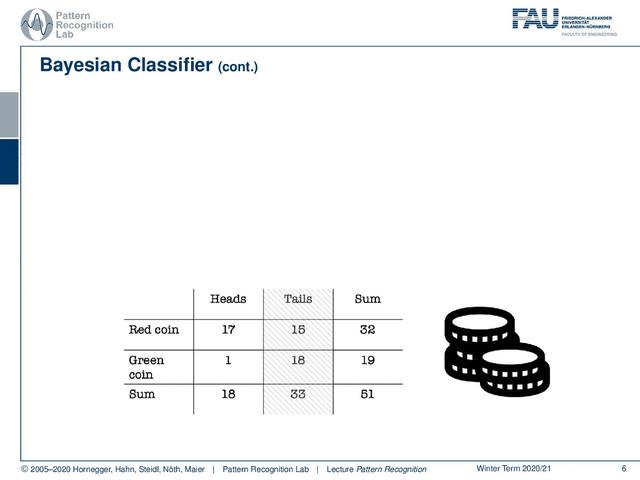
& gt模式识别讲座中CC BY 4.0下的图片。

现在我感兴趣的是找出它是红色硬币还是绿色硬币。现在，如果我看消极的一面，那么我知道我观察到了消极的一面，所以我已经可以解决这个问题了。然后我计算红币的概率，所以这是两类中的一类。另一种是绿币，你认为是45%和55%的概率。所以，如果你看反面，这不是很有力的证据，硬币实际上被扔掉了。我们来看另一个案例。

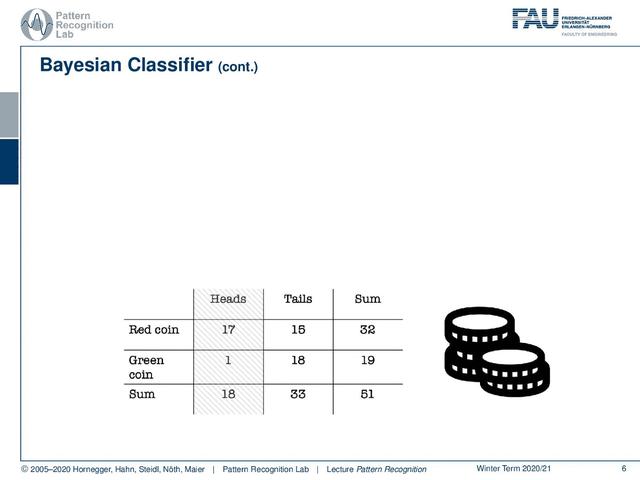
& gt模式识别讲座中CC BY 4.0下的图片。

假设我们看起来很积极。现在看正面，红币的概率大概是94%，绿币的概率只有6%。因为，当然，在大多数生产正面的情况下，都是用红币。所以，观察正面，在这种情况下，是非常有力的证据证明使用了红币。你可以看到这是一个非常典型的模式分类问题。因此，我们希望从观察到的证据中得到关于硬币的分类信息。你知道这很难。然而，如果你有这个分布，那么你可以从我们的实验中得到非常有趣和非常好的证据。让我们把它规范化。

& gt模式识别讲座中CC BY 4.0下的图片。

我们已经看到，这里X和Y的联合概率密度函数可以分解到上一个。所以用某个硬币乘以类条件概率密度函数的概率。显然，通过使用证据时间的概率，可以生成相同的联合PDF。所以你可以看到我们可以用这两个分解来表示同一个联合概率密度函数。

& gt模式识别讲座中CC BY 4.0下的图片。

现在，如果我知道这个恒等式，那么我就可以很容易地构造出所谓的贝叶斯定理。贝叶斯定理告诉我们，给定证据X的Y类概率可以表示为X给出Y的概率的阶段的概率，这个除以X的概率，现在X的概率也可以表示为整个联合概率的边缘化。现在你可以看到，很难观察到这个联合概率密度函数。但是我们可以再次使用我们的分解策略。所以我们可以看到，在这个乘以观察我们x的概率之前，这个是可以分解到所有类的，这就叫边缘化。这里的好处是我们的y总是离散的。所以我们有离散数量的类，这使我们能够把它表达为一个总和。

& gt模式识别讲座中CC BY 4.0下的图片。

这是联合概率密度函数的边缘。我们基本上可以通过边缘分析得到我们的分离。如果我们想做类似于前面Y的概率的事情，那么我们就要用X把它边缘化，如果你想这样做，那么你已经可以看到，我们必须在X的整个定义域中有一个连续的整体，因为只有在我们的情况下，或者说大多数情况下我们会在这个类中看到，X在前面的例子中不是离散的，而是一个连续的向量空。所以我们必须计算整个向量空上的积分。我们对不同概率论的简要介绍到此结束。

& gt模式识别讲座中CC BY 4.0下的图片。

在下一个视频中，我们想谈谈贝叶斯分类器，以及贝叶斯分类器与最佳分类器之间的关系。我希望你喜欢这个小视频，我期待着在下一个视频中见到你！非常感谢您的观看，再见。

如果你喜欢这篇文章，你可以在这里找到更多的短文，更多的教育资料来学习，或者看看我们的深度学习讲座。如果你将来想要更多的文章、视频和研究，我也会感谢你在YouTube、Twitter、脸书或LinkedIn上的关注。本文在知识共享4.0的归属许可下发布。如有引用，可转载修改。如果你有兴趣从视频讲座生成抄本，请尝试自动屏幕。

海因里希·尼曼:《模式分析》,斯普林格信息科学丛书4，斯普林格，柏林，1982年。

海因里希·尼曼:冯·穆斯塔恩分类，施普林格出版社，柏林，1983年。

理查德杜达，彼得e .哈特，大卫g .斯托克:模式分类，第二版，约翰威利父子公司，纽约，2000年。

(本文翻译自Joyce Xu的文章《我如何为我无法观察到的事物计算可能性？，请注明出处，原文链接:https://medium.com/data系列/how-do-I-compute-abilities-for-the-I-not-observe-5503 bde 33 ad 9)