以及案例数据来源:微信微信官方账号【我见人见我】
研究人员想知道打字训练是否能提高人的打字技能,于是对6名受试者进行了测试研究,收集了打字训练1个月、2个月、3个月前后单位时间内的错别字数量,具体如下:
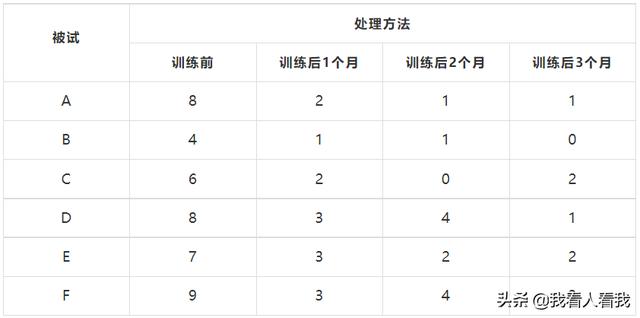
现在研究者需要检查受试者在打字训练后打字技能是否有所提高,即错别字数量是否明显下降,应该采用什么样的统计方法?
在这种情况下,因变量是单位时间内的错别字数量,这是一个数值变量。自变量只有一个,就是时间,分为四个时期:训练前、训练后一个月、训练后两个月、训练后三个月。检查打字训练后错别字数是否下降,需要比较四个时期的平均错别字数是否有差异。我们知道,如果只有一个自变量和一个因变量,可以用单因素方差分析的方法来比较三个或三个以上的总体均值。但是这里的案例与之前介绍的ANOVA “如何使用SPSS进行单向ANOVA?不同之处在于,每一个被试都参加了所有水平的自变量的检验,即得到的四组测量数据都来自同一个样本。本实验设计是心理学和医学中常用的重复测量研究设计。所以,准确地说,这种情况要用单向重复测量方差分析来检验四组均值是否相等。
重复测量研究设计(Repetitive measurement research design)又称组内设计,是指用同一组样本对同一观察变量进行两次或两次以上的测量,其中每个受试者都参与所有的测量条件,所有的测量数据都来自同一样本。基于本研究设计的方差分析是方差的重复测量分析。如果实验中只进行了两次测量,则得到两组测量数据。比较这两组数据的均值,可以采用重复测量t检验,即配对样本t检验参数检验(三):独立样本和配对样本t检验的SPSS运算。
与重复测量设计相对应的是独立样本的研究设计,也称为组间设计,是指每个实验条件由不同的被试完成,测量数据来自不同的、完全独立的样本。比如在跨文化研究中,我们比较来自中国和美国的样本数据,或者医学研究中的实验组和对照组。之前介绍的独立样本T检验和方差分析都是针对独立样本的研究设计。
1。优势
(1)有效控制个体差异的影响
在实际研究中,无论要观察的行为差异是什么,原则上都可能受到混杂变量的影响,比如个体差异。对于重复测量设计,每个被试都参与了各个水平自变量的测试,即把每个被试的测量结果与自己前后的表现进行比较,这样就可以很好地控制个体差异对测量结果的影响。
(2)提高组间效应的准确性
重复测量设计得到的结果趋于高度相关,数据变异减弱,因此显著性检验的标准差降低,统计检验更灵敏,更容易检测到较小的处理效应(即自变量引起的变异)。
(3)不需要事先对被试进行测试和筛选
在研究之前,我们在招募测试对象时都需要做测试筛选,以平衡不同测试对象所观察到的行为特征的差异,尽可能地控制这些差异所导致的测量结果的偏差。而在重复测量设计中,不同水平的测量结果都是被试与自己的比较,因此个体在某一特征上的差异已经完全平衡,不需要进行岗前测试。
(4)可观测因变量的动态变化特征
通过对同一样本在不同时期进行多次检验,可以得到因变量随时间的动态变化趋势,提取更多有价值的研究信息。
2。不足
在重复测试设计中,每个被试需要按照一定的实验顺序完成任务。例如,在上述案例中,受试者必须在训练前和训练后1-3个月进行打字测试。这种安排带来的问题是,前一次测试可能会影响被试在下一次任务中的表现,比如被试可能会变得更加熟练或疲劳,这些因素很容易与自变量混淆,成为影响因变量的干扰项。
为了解决这个问题,研究中有两种方法:
(1)随机安排实验条件的顺序;
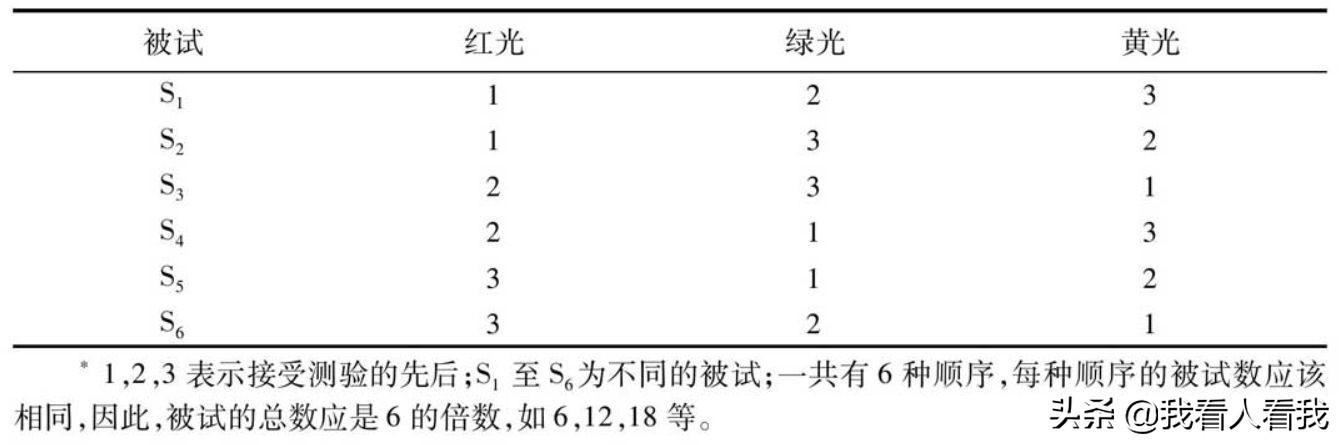
(2)用偏移平衡法消除实验顺序可能产生的影响。偏移平衡法是为了保证每一个实验条件都有相同的机会出现在各种顺序中,比如下表中的顺序排列,每个受试者在红灯、绿灯、黄灯下的测试顺序都是不同的。
三。重复测量差异分析的前提条件
1。总体服从正态分布
2。所有总体的等方差(方差的同质性)
3。样本是相互独立的
4。随机选择样本
5。符合球面假说
重复方差分析要求自变量各水平的协方差矩阵具有球面特征,即满足球面假设。因此,在重复测量方差分析中有必要对球面假设进行检验。如果不满足这个条件,方差分析的F值就会出现偏差,会增加1型错误(即“弃真”,拒绝实际成立的假设)的概率,这时就需要修正。
四。单向重复测量方差分析的SPSS操作
接下来,基于文章开头提到的打字训练案例,我将演示如何使用SPSS分析单向重复测量的方差。
研究问题:打字训练是否提高打字技能?
原假设:训练后的打字准确率和训练前没有差别。
(一)操作路径
[分析]-[一般线性模型]-[重复测量]
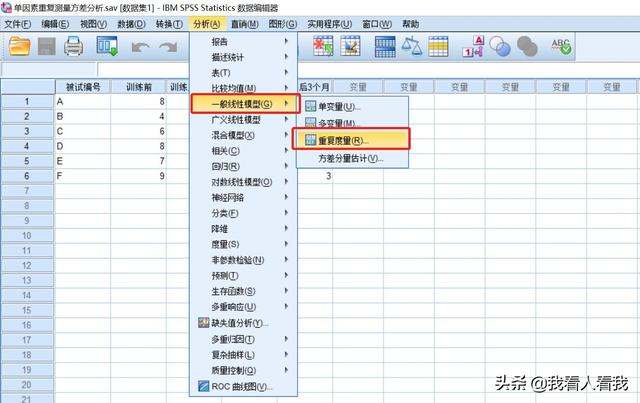
(二)定义变量
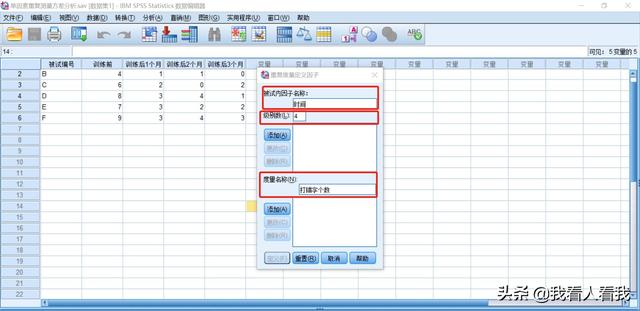
进入重复测量定义因子窗口,由于本次研究是基于时间的重复测量,因此,我们将【受试者因子名称】定义为“时间”;[级数]表示已经进行了多少次测量,这里是4次。
[测量名称]是要测量的因变量的名称。在案例中,因变量是“错别字数”,因此我们将因变量名称设置为“错别字数”
定义完变量名后,分别点击添加。
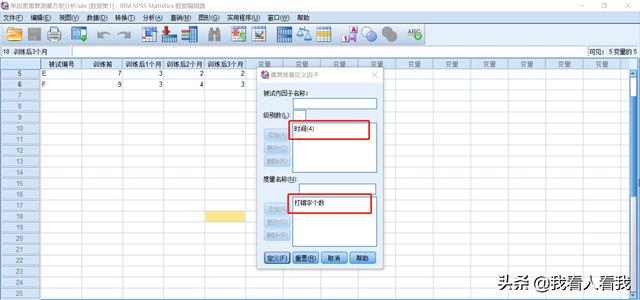
(三)选择统计数据
单击重复测量定义因子的定义按钮,打开重复测量对话框。
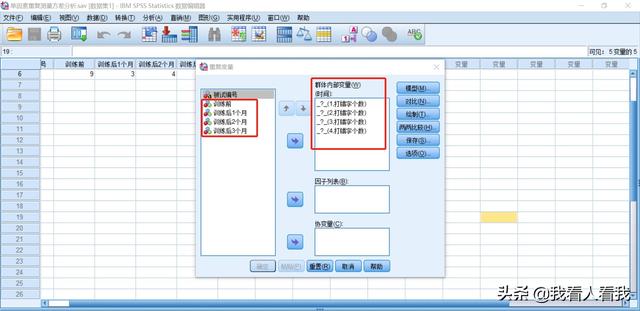
将左侧对话框中四个时间段的测量结果依次添加到[组内部变量]框中。在这里,您必须按照测量时间的顺序添加它们。
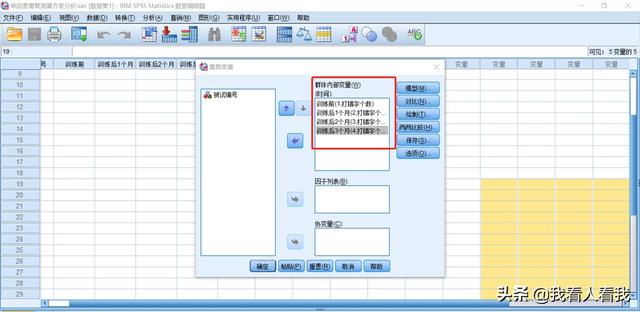
点击【重复测量】对话框中的【绘图】,打开【重复测量:轮廓图】,主要输出因变量随自变量变化的趋势图。
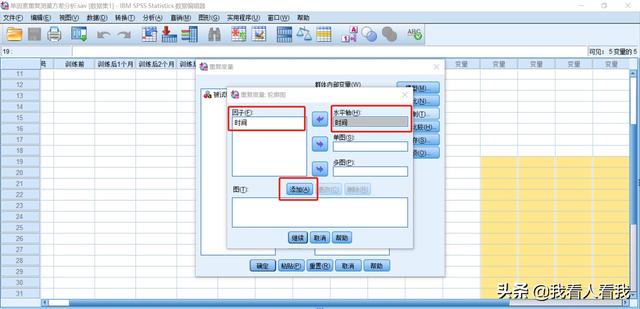
将左侧框中的【时间】添加到右侧的【横轴】框中,点击下方的【添加】,输出以测量时间为横轴的趋势图。

然后单击继续返回到[重复测量]对话框,并单击[选项]打开[多变量:选项]对话框。
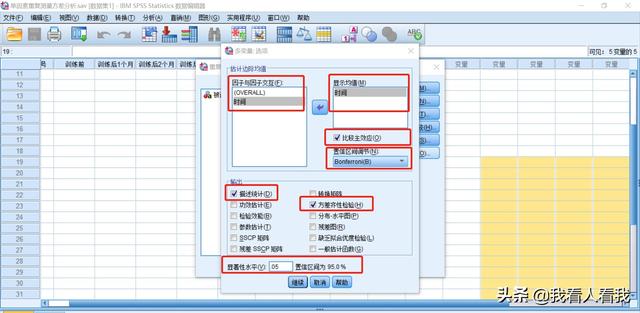
将“因子间交互作用”框中的“时间”变量添加到“显示均值”框中,勾选“比较主效应”,在“置信区间调整”中选择“Bonferroni”。Bonferroni是多重比较检验(回测)的方法,其他常用的回测方法有LSD(L)。
在[Output]框中,勾选[Description Statistics]和[Variance同质性检验]的统计量,显著性水平保持默认值0.05。
【描述性统计】输出不同自变量水平下的均值、标准差和病例数;
【方差齐性检验】就是看数据是否满足方差齐性的前提。
单击继续返回主对话框,单击确定,系统将开始运行。
(四)统计结果的解释
1。受试者内因素
内因子表告诉我们,自变量不同水平对应的标签分别是1、2、3、4。
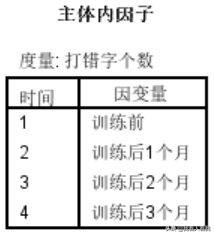
2。描述统计信息
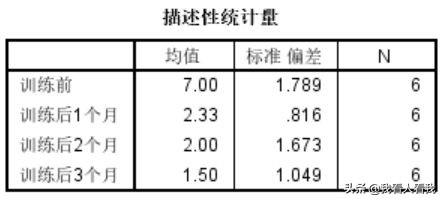
该表显示了因变量在不同自变量水平的均值、标准差和例数。从表中可以看出,训练前的错别字平均为7个,比训练后高很多,而训练后不同时期的错别字差异相对较小。但是我们不能从这个描述性的结果中得出结论,因为它可能是随机误差造成的,所以还是要看显著性检验结果。
3。球形假设检验
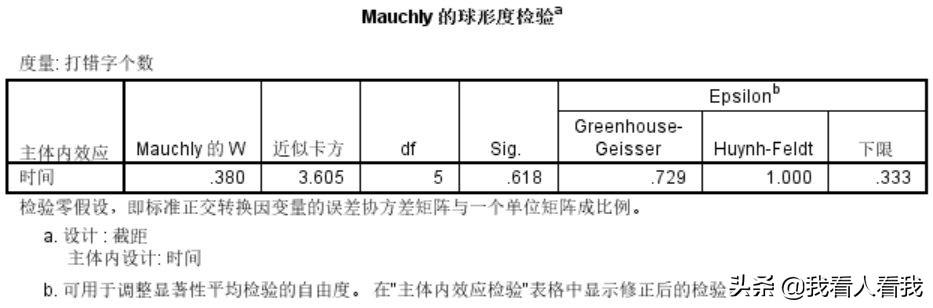
测量的重复方差分析需要满足球面假设,是否满足球面假设主要取决于概率p值(sig。栏)中。如果p值小于预定的显著性水平0.05,则意味着不满足球形假设。如果大于显著性水平,则满足球形假设。根据以上结果,在这种情况下,X =3.605,p = 0.618 >: 0.05,说明数据满足球面假设。
如果数据不满足球面假设,就需要进行ε校正。校正结果见测试结果表中的“ε”栏。SPSS提供了三种修正方法:Greenhouse-Geisser、Huynh-Feldt和Lower bound。一般来说,温室-盖瑟和惠恩-费尔特是最常用的。这两种方法得到的ε值越低,数据违背球面假设的程度越大。当ε= 1时,数据完全符合球面假设。
4。方差分析测试结果
重复方差分析的检验结果输出几个表,主要有“多变量检验表”和“被试内效应检验表”。看哪个表要看球度的测试结果。
如果数据符合球形假设,那么看“受试者内效应检查表”中第一行“假定的球形度”,根据概率p值(sig)确定不同水平的自变量均值是否存在显著差异。列)。因为这个案例的数据满足球面假设,所以我们只需要在“采用的球面度”这一行检查F值和概率P值。从下表可以看出,P
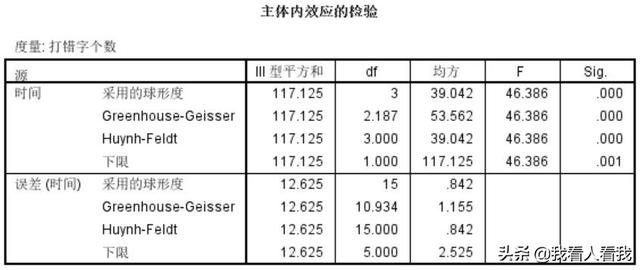
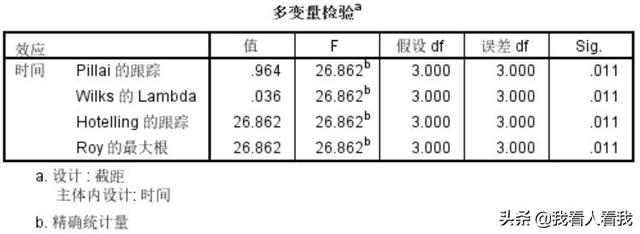
如果数据不满足球面假设,那么就要结合“多变量检验表”(如下表所示)的结果和“受试者内效应检验表”(如上表所示)的修正结果进行判断。“受试者内效应检验”的修正结果基于上述修正方法Greenhouse-Geisser、Huynh-Feldt和Lower-bound,分别对应上表中同名的三行结果。同样,是否有统计显著性也是通过比较概率p值与显著性水平来判断的。有时多变量检验的结果可能与被试内效应检验的校正结果不一致,一般以多变量检验的结果为准。
5。回溯测试
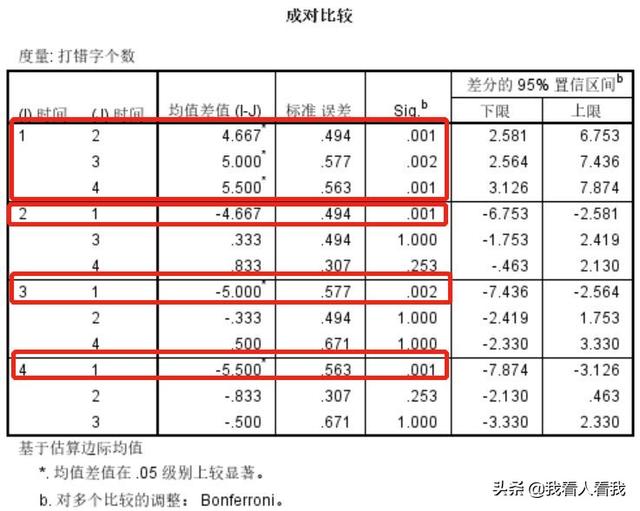
回测,又称多重比较测试和配对比较测试。方差分析的结果只能说明自变量不同水平的均值存在显著差异,而不能告诉我们哪两个水平不同,所以需要用回测来确定哪两个水平显著不同。
回测结果主要看“配对对照表”。从下表可以看出,在这种情况下,训练前和训练后1个月、2个月、3个月之间的测试显著性均小于0.05,说明存在显著差异。然而,训练后1个月、2个月和3个月之间的测试显著性大于0.05,表明没有显著差异。因此,我们可以认为打字训练可以有效地提高人们的打字技能。
6。外形图
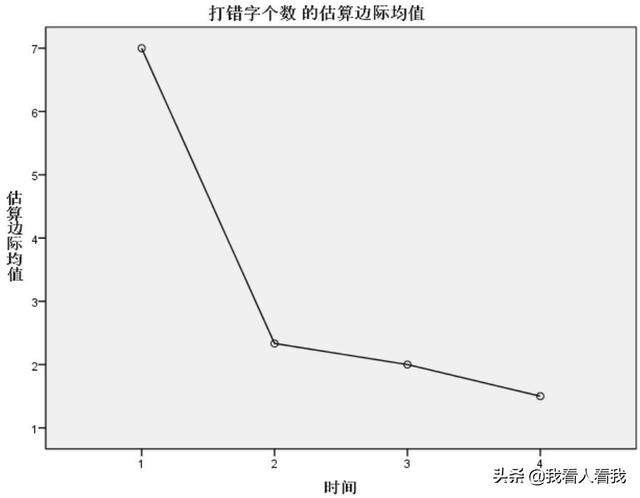
从等高线图中,我们可以直观的知道训练后的错别字数量明显低于训练前,但训练后的三次测试中错别字数量并没有明显变化,从而进一步验证了上述测试结果。
[#关于作者#] [/S2/]
中山大学人类学硕士,用户研究工程师,数据分析师,微信微信官方账号【我见人见我】,主要分享SPSS统计分析,用户研究理论与方法,社会科学研究与方法等。