作者:神雍正博

并不是所有存在于现实世界中的物质都是学校里学到的规则的形状。相反，那些规则的形状可以说只是例外或理想化。因此，对于人类来说，测量现实世界中各种复杂图形的大小是非常必要的。

日本小学的家政课会教授乌冬面、土豆丁2等简单菜肴的烹饪方法。如果你掌握了这些基本的烹饪方法，你就可以烹饪更复杂的菜肴。比如乌冬面的烹饪方法可以应用到面包、披萨或者意大利面上，从薯片中学到的方法可以扩展到土豆沙拉或者炸糕上。

如果把中小学的长方形和圆形知识比作乌冬面和土豆块，那么微积分就相当于面包、土豆沙拉等应用菜。得益于积分法，人类可以计算各种图形的面积和体积。利用积分，再奇怪的形状也能努力算出结果，真的是很大的进步。

把思维运用到实践中，用自己的力量推导出面积和体积，这就是积分的乐趣，也是学习积分的真正意义。

整合要领①:

以长方形为基础思考。

图形有很多种，其中面积计算最简单的是“矩形”。

说到这里，你是否想起小学计算初学者面积的场景？在图形面积的计算中，三角形、平行四边形、梯形、圆形等图形都是在矩形之后研究的。矩形的面积只需要“长×宽”就可以计算出来，可以说是最简单最简单的图形了。顺带一提，在数学界，正方形被视为“一种特殊的矩形”。

掌握了矩形面积的计算方法后，就可以应用到三角形的面积计算中了。另一方面，如果不知道矩形面积的计算方法，就无法计算三角形的面积。

这是因为三角形的面积可以看作是“取三角形的一个底边为边长，边高为另一边矩形面积的一半”。根据图2，三角形的面积正好是对应矩形面积的一半，也就是说“三角形的面积=底×高÷2”。

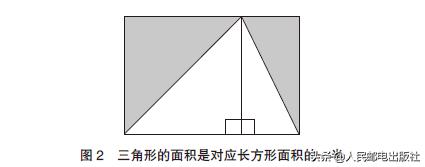
平行四边形呢？平行四边形可以看作是以平行四边形的边为底的两个三角形的组合。

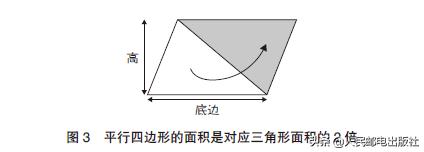
梯形呢？梯形可以看作是平行四边形的一半。如图4所示，两个相同的梯形并排组合成一个平行四边形。所以梯形的面积也是在矩形的基础上计算的，就是“(上底+下底)×高÷2”。

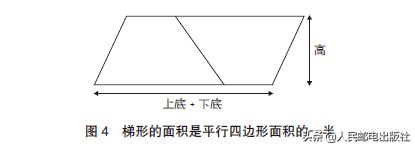
从三角形到平行四边形再到梯形，虽然这三种图形看似没有直接关系，但它们的面积公式都是基于矩形面积推导出来的。

整合要领②:

把图形想象成小矩形的组合。

你在小学的算术课上做过以下事情吗？如图5，用圆规在方形纸上画一个圆，然后数圆内的正方形个数。之后，画几个大小不一的圆，数这些圆里有多少个正方形。

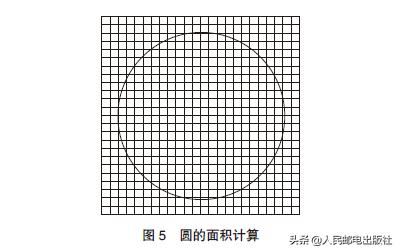
这个赋值其实和圆的面积公式有关。圆面积的公式是“半径×半径× 3.14”，其中3.14是圆周率的近似值，“试方块数”是解释圆周率求导的一种方法。

这里，我们再来回顾一下这个方法。

我们先来数数图6中半径为2 cm的圆里有多少个正方形3(正方形的边长为1 mm)。这种方法虽然有些不准确，但可以让小学生更容易理解。

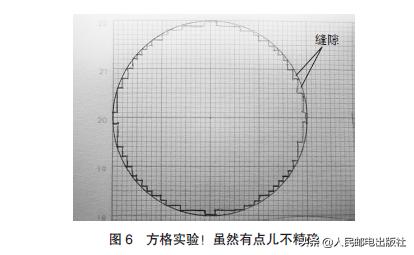
图6圆里有1189个正方形，就面积而言是11.89 cm2。

圆的面积公式是“半径×半径×π”。在网格实验中，我们的目的是求圆周率，所以可以对这个公式进行变形，得到“圆周率=面积÷(半径×半径)”。在图6的例子中，圆的半径是2，所以面积除以2的4次方，pi是2.972 5。

相比3.14，这个成绩实在是太小了。虽然很可惜，实验是

像这样。即便如此，我们还是会明白一件事，那就是“圆周率，也就是π，大致是一个接近3的数”。

如果细分正方形或者放大圆，圆内正方形面积之和会逐渐逼近圆面积公式“半径×半径× 3.14”，即圆周率。

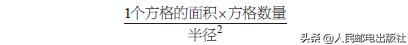
会逐渐逼近3.14。这样，用正方形的个数代替圆的面积，逐渐接近评价的方法，就叫做“近似法”。我小学也做过这个实验。几十年后的今天，我依然清晰地记得自己尝试数方块得到答案后心中的满足感。

对了，可能有人会有以下疑问。

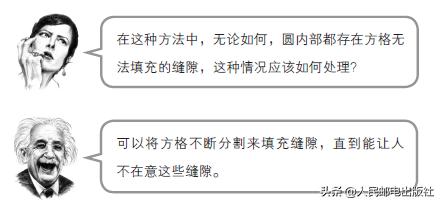
博士的回答是老师惯用的方法，但是有点忽悠人。因为这个回答会留下下面的问题。

“不在乎这些差距”到底是什么意思？其实不管你在乎不在乎，总会有差距不是吗？

这个问题看似枯燥，但却是高等数学中一个很有趣的问题。综上所述，为了解决上述问题，我们有必要利用“夹点定理”(双面夹点定理)从圆的内外来研究图形。即先算出“圆内的方块数”对应的pi，再用同样的方法算出“包含圆边界的方块数”(内部的方块数加上包含圆边界的方块数)对应的pi。这样，我们可以得到以下结论:

对应于圆内正方形数量的pi <圆的实际pi <对应于包括圆边界的正方形数量的pi

如果不断用更小的正方形替换正方形，那么“圆内正方形个数对应的π”和“包括圆边界在内的正方形个数对应的π”的值会逐渐接近，两者都接近圆的实际π，这就是“夹点定理”。

在微积分中，不拘一格的精神同样重要。

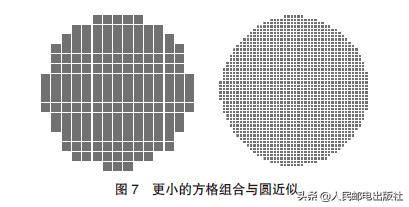
图7是由小方块组成的类似圆形的图形。左边有一个大广场，右边有一个小广场。从这两个图形中，我们大概可以理解为“如果把粗略的图形细化，就会接近实际的图形(圆)”。精度非常高的锯齿形图形实际上很难从视觉上与光滑图形区分开来。

电视和电脑的液晶显示器都是利用这个原理来显示画面的。液晶显示器显示的图像实际上是锯齿状的。但是显示器中锯齿的精细度很高，所以我们眼中看到的是流畅的线条。

我们也可以说，圆实际上是由无数个细方块组成的锯齿状图形，即圆是锯齿状图形的“极限”。像这样，“逼近”是数学中极其有用的方法。

如果你坚持完美再现流畅的线条，那就不会有LCD了。得益于不完善的近似方法，划时代的技术诞生了。

计算圆的面积时，小学用的方法是用“正方形”划分圆的内部空。这样做的原因其实很简单，就是方纸的正方形就是正方形。

求圆的面积的关键是把圆细分。也就是说，划分的形状不应该局限于正方形。所以我们可以把圆分成“细长的短条”来计算面积。比如在图8中，我们尝试把圆分成细长的条，也就是长方形的组合。

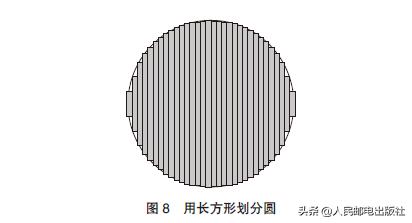
说了这么多，既然说的是符号，那就从现在开始尽量用整数符号吧。公式也会从这里出现，但内容与刚才的解释完全一致，请大家轻松阅读。就像业内人士用行业术语说话一样，用数学符号来解释数学，同样的内容在表达上会显得很优雅。

在图9中，我们将圆切割成非常窄的条。水平方向是x轴。此时，圆的切割方向与X轴正好垂直。

在此基础上，我们选取一个宽度为δ x的短条，δ是一个希腊字母，读作“Delta”，常用作“不同”的符号，代表一个很小的数。

现在，我们用公式来表示这个短杆的面积。

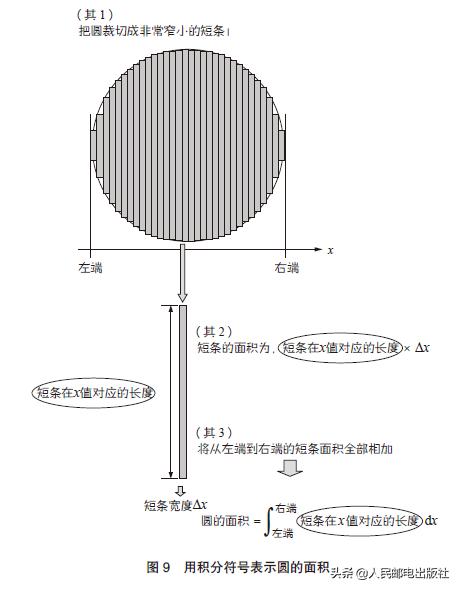
短条面积= x值对应的短条长度× δ x

如果你问为什么要计算短条的面积，那是因为我们需要从这里计算圆的面积。把这些细长条的面积加起来，就得到圆的面积。具体来说，就是把所有的短条从左端加到右端就可以了。

这里，我们逐渐将短条的宽度减小到不能再减小的程度。这样，短条看起来更像一条“线”，而不是长方形。无数条“线”加在一起，结果逐渐逼近“圆的面积”。如果用整数符号表示，可以写成以下形式。

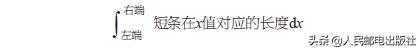
在公式中，像字母S的纵向拉长这样的符号听起来和integral是一样的。积分的原意是“和”，所以积分符号也取自拉丁语单词“和”的首字母S。这是由一位名叫莱布尼茨的数学家(也是哲学家)提出的。

这里我简单加一点delta (δ)和d。

和δ d，两者都源于“不同”。两者的区别在于 δ是“近似值”，英文小写字母D是“精确值”。

“精确值”是什么意思？比如pi，3.14是它的近似值，无限循环的3.141 592 653 589 793 238 462 643 383 279是它的“精确值”。近似值在某些情况下肯定是不正确的，而精确值在任何情况下都是正确的。

所以我们可以这样理解dx:“把原来由短杆宽度δ x计算出来的值，看作是趋于零的‘精确值’。”

综上所述，delta (δ)和英文小写字母D分别用于以下几种情况。

delta(δ)-当有宽度时(宽度大于0)。

英文小写字母d-当宽度接近0时，计算极限值。

另外，虽然微积分中会出现各种公式和符号，但是初学者一开始不懂这些东西也没关系，δ和d也是一样。

简单微积分:学校没教过的超简单初学技巧作者:神雍正博

这本书是微积分初学者的通俗读物。重点讲解微积分的思维方法，用生活实例讲解微积分的基本原理、公式推导和实际应用意义，解答微积分初学者遇到的常见困惑。这本书讲解循序渐进，生动亲切，没有繁琐的计算和干巴巴的理论。是一本只需轻松阅读就能理解微积分原理的入门书。