有未知数的方程就是方程。数学最早发展于计数，通过数与未知数之间的加减乘除和幂等运算组合形成代数方程组:一元线性方程组、一元二次方程组、二维线性方程组等等。但随着函数概念的出现和基于函数的微分、积分运算的引入，方程的范畴更广，未知数可以是函数、向量等数学对象，运算不再局限于加减乘除。

方程问题

方程在数学中占有重要地位，似乎是数学永恒的话题。方程的出现不仅大大扩展了数学的应用范围，而且解决了许多算术解法无法解决的问题，对后来整个数学的进步产生了巨大的影响。尤其是数学上的许多重要发现都与它密切相关。示例:

方程怎么解？

中学的方程基本都是这一类，方程中的未知数可以出现在分数、代数式、根、三角函数、指数函数等初等函数的自变量中。例如以下形式(x未知):

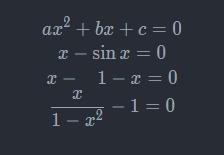
代数方程

与上述方程不同的是，方程中的未知数是函数本身，而不是函数的自变量。运算涉及加减乘除和函数复合。例如:

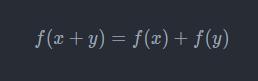
函数方程

函数方程的求解没有统一的理论和通用的方法。对于部分函数方程，考虑:

傅里叶变换

由于数学从常数数学变成了变量数学，方程的内容丰富了，因为数学引入了更多的概念和更多的运算，从而形成了更多的方程。其他自然科学尤其是物理学的发展也直接提出了方程求解的需求，并提供了大量的研究课题。

微分方程是指含有未知函数及其导数的方程。这类方程的未知数是函数。与函数方程不同的是，对于未知函数有导数运算，可以是高阶导数。但如果方程中的未知函数只包含一个自变量，那么该微分方程就是常微分方程。

一般n阶常微分方程的形式:

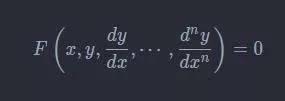
函数方程

如果方程左端的函数Y及其导数都是一阶有理代数表达式，则该方程称为N阶线性微分方程，否则为N阶非线性微分方程。

因为大部分微分方程无法得到显式解，所以只能分析其解的稳定性或者寻找近似的数值解。这一部分内容丰富，充满活力，有很多工作要做。

如果微分方程中的未知函数是多元函数，并且存在未知函数的偏导数运算，则该方程称为偏微分方程。

17世纪，微积分建立后，常微分方程的相关理论迅速发展。常微分方程也被应用到几何和力学问题的讨论中，并解释早期已经知道的天体力学中的事实，获得新的发现。但是，偏微分方程的研究较晚。物理学中遇到的偏微分方程的一些问题在18世纪创造了一个分支——数学物理方程，直到19世纪末，偏微分方程的一般理论基础才发展起来。

偏微分方程

偏微分方程与其他数学分支如泛函分析、函数论、拓扑学、代数学、复分析等密切相关。这些数学分支中的基本概念、思想和方法得到了广泛的应用。

通常，积分符号下含有未知函数的方程称为积分方程，如果未知函数是多元函数，则方程称为多维积分方程。

考虑随机过程的随机微分方程引入了随机项或马尔塞夫链，使得方程更加复杂。