今天我们来讲解一下高中与积分相关的知识要领。微分知识我们已经讲过了，有需要的话可以看看我之前关于微分的文章，积分其实就是微分的反算过程。

一、积分的定义

假设:

，那么将函数与X积分，其实就是求这个微分函数的原函数。积分的数学表达式是:

是的，它是一个微分函数。为什么它的积分多了一个C常数？原因很简单，因为任何常数的微分都是零，所以我们在求微分函数的原函数时，需要加上一个任意常数。可以看出，函数的积分函数的解不是唯一的，因为C可以取任意常数。所以我们真正计算积分的时候，都是用固定范围的x个区间来计算定积分。

二。定积分

微积分基本定理:

如果是微分函数，是有的。

上面提到的微积分基本定理，而上面提到的公式也叫做牛顿-莱布尼茨公式。上面公式的意思是，在[a，b]区间内对函数进行积分，等于B点的原函数值减去a点的原函数值，细心的同学可能会发现常数c缺失的原因。那是因为减去了两个常数C，正好是相减，这样定积分就有了定解。

三。积分的基本公式

，可以导出下面的公式:

，可以导出下面的公式:

，可以导出下面的公式:

以上提到的基本积分公式就这些了。直接背下来就行了。虽然看似公式很多，但其实很多都是常识性的公式，并不难记。

四。积分面积

如果是平面曲线方程，那么由曲线f(x)和直线x=a，x=b，y=0围成的面积可以由下式求出。例如下面的曲线:

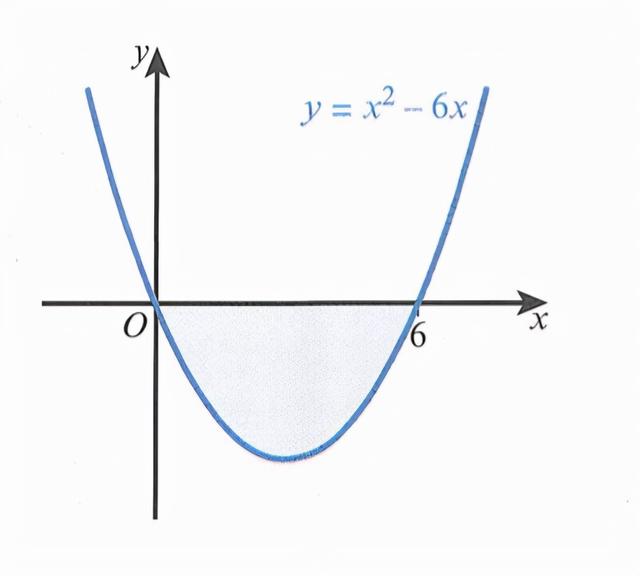
由曲线和直线x=0、x=6和y=0包围的阴影部分的面积由积分表示如下:

如果找到两条曲线f(x)和g(x)，则X在[a，b]中的面积如下:

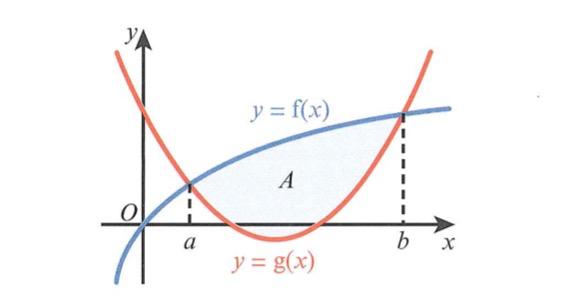
则计算公式为:

这里需要强调的是，同学们不要看到所有的公式都是为了积分，就僵化到只觉得可以积分，只是一个代号，实际上是可以的。所以函数也可以转化为X关于Y的函数，然后就有了，也就是说我们不仅可以计算曲线与X轴相交的值域的面积，还可以计算曲线与Y轴相交的面积，然后将函数关系转化为对Y的积分.如下面的曲线:

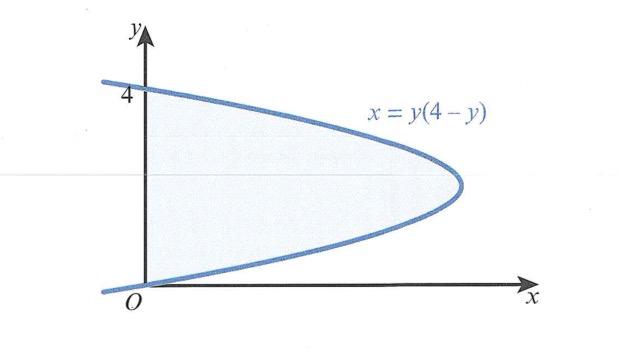
求曲线和Y轴的相交面积，其实就是计算积分。

积分面积计算注意事项:

这里需要注意的是，面对用积分计算面积的问题，核心是找出目标面积的加减关系，然后用积分找出每一部分可以计算的面积，再加减得到目标面积。同时需要注意的是直线也是曲线方程，只是一个特殊的曲线方程，也可以用积分公式计算面积。同时注意，题目中往往没有明确给出线性方程，可以根据图上的坐标数据自己解出线性方程。

四。整数体积

曲线，绕X轴转动360度，在x=[a，b]区间内形成的三维立体的体积为:

曲线，绕Y轴转360度，在区间y=[a，b]中形成的三维立体的体积为:

你看到了吗，积分的强大之处在于它可以精确计算不规则平面的面积和不规则立体的体积，前提是你可以用方程对这些曲线建模，得到它们的抽象方程，那么计算出来的面积和体积就是因此，我们工程应用的核心就是建立目标物体的抽象方程。

好了，以上就是整个高中的积分知识要领。看完这篇文章，可以说你已经学会了整个高中的积分知识。看完之后，你就掌握了整个高中的积分知识。希望能帮助你提高对积分知识的理解。同学们，慢慢消化吧。感谢您的阅读。下次见。