牛顿365，不定积分的概念和性质；原函数存在定理

2014年3月20日，网友“仁心326医生”上传了一篇题为《不定分的概念和性质》的文档。

…不，定积分积分积分定积分不定积分:见牛顿353 ~ 364 …

....概念，想法:见欧几里得22，23...

(…欧几里德:小说名…)

....性、质量和自然:见欧几里德37...

文件内容:…

…内容，内容:参见欧几里德66 …

第四章第一节不定积分的概念和性质

一、不定积分的概念

二、基本积分表

…基础，基础，基础:参见欧几里德2 …

三、不定积分的性质

一、不定积分的概念

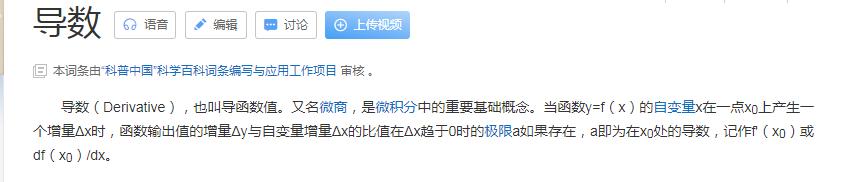
1定义如果可导函数f(x)的导函数在区间I内是F(x)[即对于任意x∈I，有:F'(x)=f(x)或dF(x)=f(x)dx]，则函数F(x)是I内F(x)的本原。

…定义、意义和定义:参见欧几里德28 …

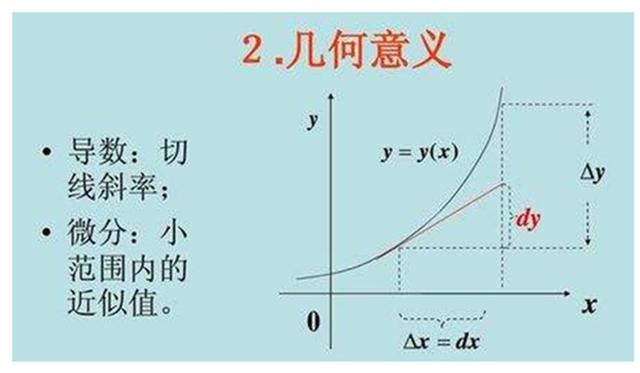
…可导:若f(x)在x0处连续，当a趋于0时，[f(x0+a)-f(x0)]/a有极限，则f(x)在x0处可导…见牛顿360 …

....函数，数字和函数:参见欧几里德52...

∈:数学符号“属于”…参见牛顿303 …

(…符号，符号:见欧几里德160，161 …)

...d:差异首字母...

【微分(英语):n .(名词)差；差异；价格差异；工资差别(尤指同一行业不同工作的)。

(形容词)微分的；视差异而定；这是有区别的。

——牛顿321

dx是什么意思？？——网友提问

2019-09-07，想玩游戏的猫:d(x)代表区分x。

dy/dx中的d表示“微增量”，即微增量Y除以微增量x，在函数中表示微分。

Dx是X的微分，是增量的细化，dx是很小的X。

——牛顿3】

例子

(x ^ 3/3)' = x ^ 2 x ^ 3/3是x ^ 2在(——∞，+∞)上的原函数；

…:电源…

....x ^ 3:x的三次方...

(sin x)'=cos x sin x是cos x在(——∞，+∞)上的原函数。

原函数存在定理；

…定义、原理和定理:参见欧几里德2 …

…原函数的存在定理:又称积分上限函数的导数定理…参见牛顿361 …

区间内连续函数必有原函数。

…连续的，连续的:参见欧几里德44 …

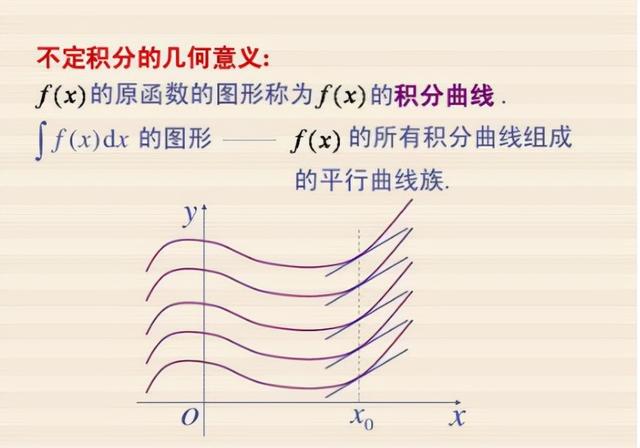
如果一个函数有原函数，显然它的原函数不唯一。

例子

(x ^ 3/3+1)' = x ^ 2，其中x ^ 3/3+1是x ^ 2的原函数；

(x ^ 3/3+2)' = x ^ 2，其中x ^ 3/3+2是x ^ 2的原函数；

结论:X ^ 3/3+C(其中C为任意常数)是X ^ 2的原函数，是它的全部原函数。

....常数，数字和常数:见欧几里德132...

定理1如果f(x)是F(x)在区间I中的原函数，那么F(x)+C(C是任意常数)是F(x)在I中的整原函数。

证书

....证明，澄清和证明:见欧几里德6...

设φ (x)是f(x)在I上的任意原函数[即对于任意x∈I，有φ' (x) = f (x)]，则:

[φ(x)-F(x)]' =φ'(x)-F '(x)= F(x)-F(x)= 0

“这里应用的是导数法则，函数之和的导数等于每个函数的导数之和。”现代学者说。

....φ:第21个希腊字母。发音:fài…参见牛顿359 …

“设f(x)和g(x)可导，则[f (x) g (x)]' = f' (x) g' (x)。

请看下集“/s2/]牛顿366，导数的四种算法[/s2/]”

不了解历史，就看不清未来。

欢迎来到头条“人性的游戏”