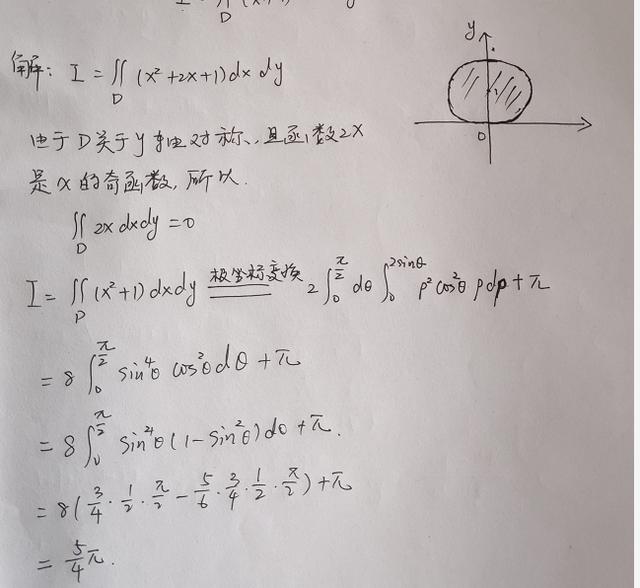考研要掌握二重积分的计算方法(直角坐标，极坐标)，二重积分的计算公式如下:

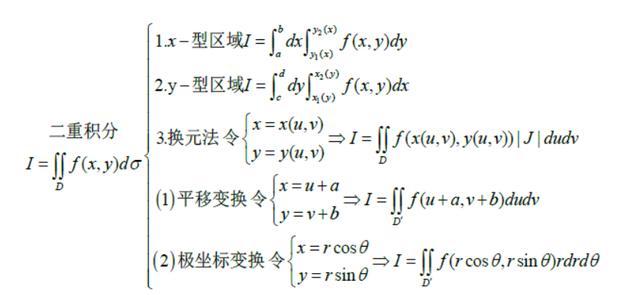
二重积分的计算主要在于将二重积分转化为重复积分计算。转化为重复积分计算时，坐标系的选择不仅取决于积分域D的形状，还取决于被积函数的形式。

(1)适用于极坐标计算的二重积分被积函数一般应具有以下形式:

f(y/x),f(x/y),f((x^2+y^2)^(1/2))

它们之所以适用于极坐标，是因为它们可以转化为极坐标中R或thetha的一元函数。

(2)适用于极坐标计算的二重积分的积分域一般应具有以下形状:

圆、圆或它们的一部分(如扇形)在中心原点；用穿过原点或其一部分的边界圆来圆化中心坐标轴上的区域。

计算二重积分时有时需要利用被积函数的奇偶性和积分区域的对称性。常用的结论如下:

(1)利用积分域的对称性和被积函数的奇偶性:

(2)利用变量的对称性:

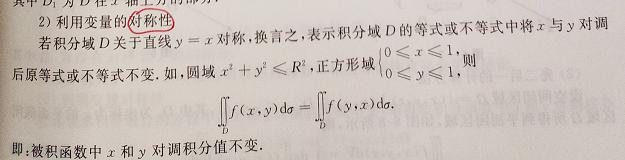
问题1:计算直角坐标下的二重积分

示例1:

解法:先画积分域D，不难看出积分域是关于两个轴对称的，被积函数也有奇偶性，所以要利用对称性和奇偶性。

解决方案:

问题二:用极坐标计算二重积分

示例2:

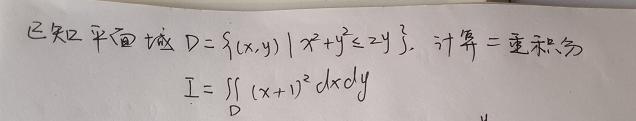
解法:积分面积D关于Y轴对称左右对称，被积函数(x+1)2 = x ^ 2+2x+1，其中2x为x的奇函数，x ^ 2+1为x的偶函数，先用奇偶化简，再用极坐标计算。

解决方案: