在实际工程中,应用最广泛的调节器控制规律是比例、积分和微分控制,简称PID控制,也称为PID调节。PID控制器因其结构简单、稳定性好、运行可靠、调节方便而成为工业控制的主要技术之一。
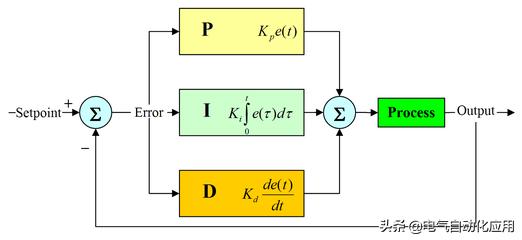
PID控制是一种传统的控制方法,适用于温度、压力、流量、液位等几乎所有的现场。在不同的现场,只需对PID参数进行不同的设置,只要参数设置得当,就能取得良好的效果。可以达到0.1%甚至更高的控制要求。
今天,我给大家做一个理论上的解释。在下面的文章中,我将讲解西门子S7-200、S7-300和薄涂PLC如何使用PID控制,以及如何编程和注意事项!
喜欢的请关注!
那么什么是PID控制呢?
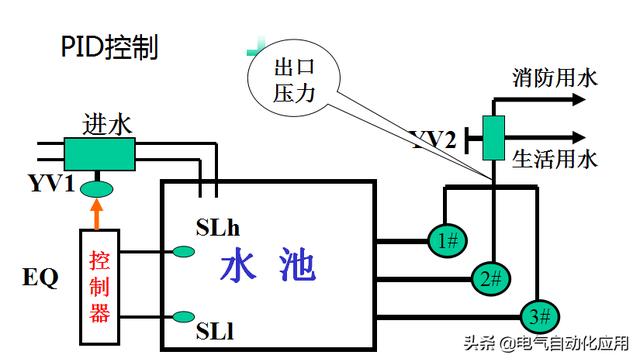
我先举个例子吧!
一、PID的故事
小明接到这样一个任务:一个水箱漏水(而且漏水的速度不一定恒定),要求水面高度保持在一定位置。一旦发现水面高度低于要求位置,应向水箱加水。
接到任务后,小明一直守在水箱旁。时间长了,他觉得无聊,就跑到房间里看小说,每30分钟检查一次水位。水漏得太快。小明每次来检查,水都漏出来,远远达不到要求的高度。小明每3分钟换一次检查。结果每次水都不怎么漏,也不用加水。他经常做的事情是无用的。几次测试后,确保每10分钟检查一次。这个检查时间称为采样周期

起初,小明用勺子加水。水龙头离水箱有十几米远,经常要跑好几趟才能加够水。于是小明改用水桶加水。一加是个桶。跑的次数少了,加水的速度更快了。但是,有几次,水箱溢水,鞋子不小心湿了。小明又用脑了。我不需要勺子或水桶。老子用的是盆。几趟下来,发现刚刚好,不用跑太多次。这个浇水工具的大小叫做比例因子
小明还发现,虽然水不会过度溢出,但有时会高于要求的位置,仍然存在湿鞋的危险。他想了另一个办法,在水箱里装一个漏斗。每次他不是直接把水倒进水箱,而是倒进漏斗,让它慢慢加。这个溢出问题已经解决了,但是加水的速度比较慢,有时候跟不上漏水的速度。于是他试着换不同大小的漏斗来控制加水的速度,最终找到了满意的漏斗。漏斗时间称为积分时间
小明终于松了一口气,但任务的要求突然严格起来,水位控制的时效性大大提高。一旦水位过低,必须立即将水加到要求的位置,不能过高,否则发不出工资。小明又尴尬了!于是他又努力工作,终于让它想到了一个办法。他经常在身边放一盆备用水。他发现水位低了,就会带着一盆水下去,不经过漏斗,这样时效性就有保证了,但有时候水位会高很多。他在水面上凿了一个略高于所需水位的洞,然后在下面的备用水桶上接了一根管子,这样多余的水会从上面的洞里漏出来。漏水的速度叫做微分时间。
看到几个问采样期的帖子,临时想到了这个故事。微分的类比有点牵强,但能帮助理解,呵呵,入门级,如果能帮助新手理解PID,就够了。故事中,小明的实验是一步一步独立完成的,但实际加水工具、漏斗直径、溢流孔大小都会同时影响加水速度和水位超调大小。做了后面的实验后,经常会修改前面实验的结果。
故事中,小明的实验是一步一步独立完成的,但实际加水工具、漏斗直径、溢流孔大小都会同时影响加水速度和水位超调大小。做了后面的实验后,经常会修改前面实验的结果。
PID控制方式下,用水壶往杯子里倒半杯水带刻度后停止;
设定值:水杯半杯刻度;
实际值:杯中的实际水量;
输出:从水壶中倒出的水和从杯子中舀出的水;
测量:人眼(相当于传感器)
执行人:人
执行:倒水。
反向:舀水
(1)P比例控制
即人们看到水杯中的水量没有达到水杯刻度的一半,就按照一定的水量或者水杯中的水量超过刻度,从水壶中的国王水杯中倒水,用一定的水量从水杯中舀水。这个动作可能会导致少于半杯或多于半杯停止。
描述:
比例控制是最简单的控制方法。控制器的输出与输入误差信号成比例。当只有比例控制时,系统输出中存在稳态误差。
(2)PI积分控制
即在杯中倒入一定量的水。如果发现杯子里的水量没有刻度,就会一直倒。后来发现水量超过半杯,就从杯子里舀水到外面,不够就反复倒水,多了就舀水,直到水量达到刻度。
描述:
在积分I控制中,控制器的输出与输入误差信号的积分成比例。对于一个自动控制系统来说,如果进入稳态后还有稳态误差,则称控制系统有稳态误差或简称系统有稳态误差。为了消除稳态误差,必须在控制器中引入“积分项”。积分项对的误差取决于对时间的积分,随着时间的增加,积分项会增加。这样,即使误差很小,积分项也会随着时间的增加而增加,从而推动控制器的输出增加,进一步减小稳态误差,直至等于零。因此,比例+积分(PI)控制器可以使系统进入稳态后无稳态误差。
(3)PID微分控制
也就是人的眼睛看杯子里的水量和刻度之间的距离。差距大的时候,他们就用水壶里的大量水倒水。当人们看到水量接近刻度时,就减少水壶中的水量,慢慢接近刻度,直到停留在杯中的刻度处。最后,如果它能准确地停在标尺的位置,它就是无静差控制;如果你停在秤附近,有静态误差控制。
描述:
在微分控制D中,控制器的输出与输入误差信号的微分(即误差的变化率)成比例。
在工程实践中,应用最广泛的调节器控制规律是比例、积分和微分控制,简称PID控制,也称为PID调节。PID控制器已有近70年的历史。由于其结构简单、稳定性好、运行可靠、调节方便,已成为工业控制的主要技术之一。当不能完全掌握被控对象的结构和参数,或不能获得精确的数学模型,而控制理论的其他技术又难以采用时,必须通过经验和现场调试来确定系统控制器的结构和参数。这时候应用PID控制技术是最方便的。即当我们对一个系统和被控对象不完全了解,或者不能通过有效的测量手段得到系统参数时,PID控制技术是最适合的。PID控制,其实也有PI和PD控制。PID控制器是以系统误差为基础,利用比例、积分和微分来计算控制量进行控制。
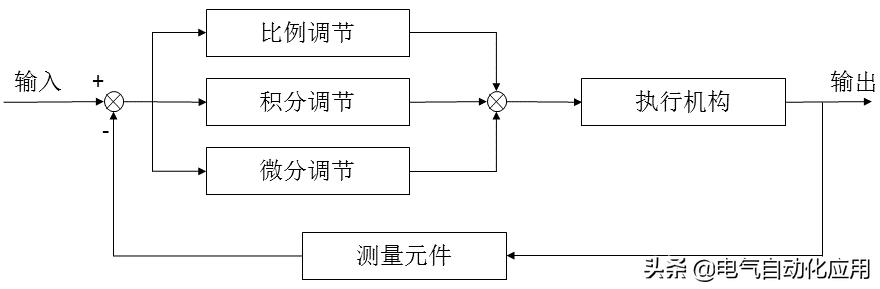
PID参数
(1)比例(P)控制
比例控制是最简单的控制方法。控制器的输出与输入误差信号成比例。当只有比例控制时,系统输出中存在稳态误差。
(2)积分(I)控制
在积分控制中,控制器的输出与输入误差信号的积分成比例。对于一个自动控制系统来说,如果进入稳态后还有稳态误差,则称控制系统有稳态误差或简称系统有稳态误差。为了消除稳态误差,必须在控制器中引入“积分项”。积分项对的误差取决于对时间的积分,随着时间的增加,积分项会增加。这样,即使误差很小,积分项也会随着时间的增加而增加,从而推动控制器的输出增加,进一步减小稳态误差,直至等于零。因此,比例+积分(PI)控制器可以使系统进入稳态后无稳态误差。
(3)微分(D)控制
在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成比例。自动控制系统在克服误差的调节过程中,可能会出现振荡甚至失稳。原因是有大惯性分量(环节)或延迟分量,可以抑制误差,它们的变化总是滞后于误差的变化。解决方法是“提前”误差抑制函数的变化,即当误差趋近于零时,误差抑制函数应为零。也就是说,在控制器中仅引入“比例”项往往是不够的。比例项的作用只是放大误差的幅度,目前需要增加的是“微分项”,可以预测误差的变化趋势。这样,比例+微分的控制器可以提前使抑制误差的控制效果等于零甚至为负,从而避免被控量的严重超调。因此,对于大惯性或大滞后的被控对象,比例+微分(PD)控制器可以改善系统在调节过程中的动态特性。
如果在PID参数调整时,有一种理论上的方法来确定PID参数,当然是最理想的方法。然而,在实际应用中,更多的是采用试凑法来确定PID参数。
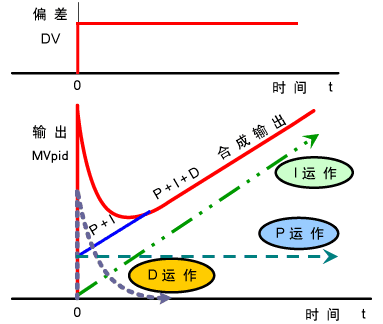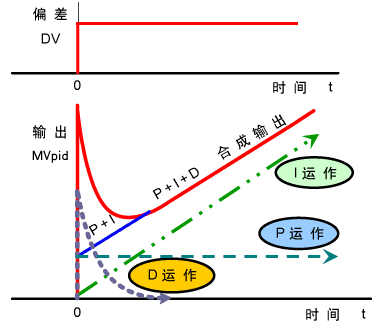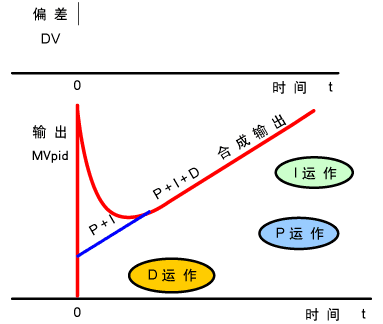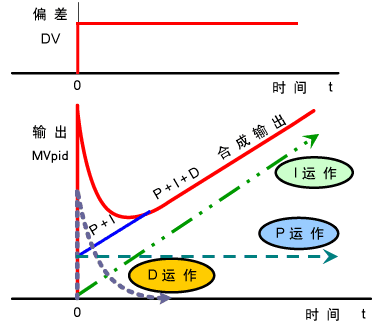
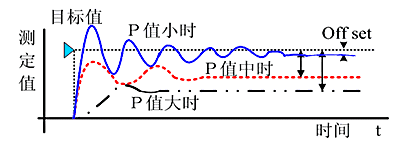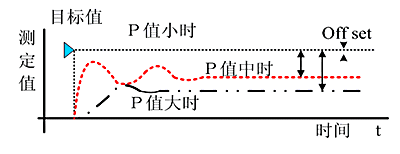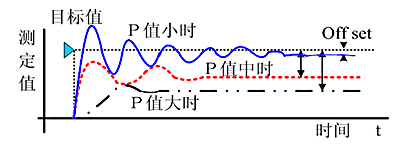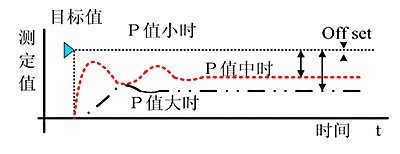
增大比例系数p一般会加快系统的响应速度,有静态误差时有助于减小静态误差。但如果比例系数过大,系统会有较大的超调,产生振荡,恶化稳定性。
增加积分时间I有利于减小超调和振荡,增加系统的稳定性,但系统静态误差的消除时间变长。
增加微分时间d有利于加快系统的响应速度,减小系统的超调量,增加稳定性,但系统抑制扰动的能力减弱。
在试运行中,可以参考上述参数对系统控制过程的影响趋势,实行先比例、后积分、再微分的设定步骤进行参数调整。
PID控制器参数整定方法
PID控制器的参数整定是控制系统设计的核心内容。根据被控过程的特点,确定PID控制器的比例系数、积分时间和微分时间。整定PID控制器参数的方法有很多,可以归纳为两类:
一、理论计算和设定方法
它主要是根据系统的数学模型,通过理论计算来确定控制器参数。这种方法得到的计算数据不一定能直接使用,必须通过实际工程进行调整和修改。
二。工程设置方法
主要依靠工程经验,直接在控制系统的测试中进行。该方法简单易掌握,在工程实践中应用广泛。PID控制器参数的工程整定方法主要有临界比例法、响应曲线法和衰减法。三种方法各有特点。它们的共同点是通过测试后根据工程经验公式整定控制器参数。但无论采用哪种方法,控制器参数都需要在实际运行中最终调整和完善。
现在一般采用临界比率法。使用该方法整定PID控制器参数的步骤如下:
(1)首先,预先选择足够短的采样周期以使系统工作;
(2)仅加入比例控制环节,直到系统对输入的阶跃响应出现临界振荡,记录此时的比例放大系数和临界振荡周期;
(3)在一定的控制程度下,通过公式计算PID控制器的参数。
PID参数的设定:是依靠经验和对过程的熟悉,参考测量值跟踪和设定值曲线来调整P、I、D的大小。
常用公式:
找到最佳参数设置,从小到大检查;
先比例后积分,再加微分;
曲线震荡频繁,比例带盘面要放大;
曲线围绕大湾浮动,比例带盘转向小盘;
曲线偏离缓慢,积分时间减少;
曲线波动周期越长,积分时间越长;
第一步,设定比例控制
将比例控制函数由小变大,观察每次响应,直到得到一条响应快、超调小的响应曲线。
第二步,积分环节
如果比例控制下稳态误差达不到要求,则应增加积分控制。首先将上一步选择的比例系数降低到原始值的50 ~ 80%,然后将积分时间设置为较大的值,观察响应曲线。然后,减少积分时间,增加积分函数,相应调整比例系数,反复尝试,直到得到满意的响应,从而确定比例和积分的参数。
第三步,设置差分链接
如果通过以上步骤,PI控制只能消除稳态误差,动态过程不尽如人意,则应加入微分控制,形成PID控制。先设定微分时间TD=0,逐渐增大TD,同时相应改变比例系数和积分时间,反复尝试,获得满意的控制效果和PID控制参数。
PID的15个基本概念[/S2/]
没有金刚钻,没有瓷器。为了掌握和应用PID,我们非常有必要学习基本概念来武装自己。有些概念会搭配实际项目中常用的表达方式,从“实:”开始。
1调整量:反映调整对象实际波动的量。调节量总是在变化。
实际:通常由检测到的反馈值表示,如yout(t)。
2设定值:PID调节器的设定值是人们期望被调节量达到的值。设定值可以是固定的或可变的。
实际:人为设定,常用rin(t)表示。
3控制输出:PID调节器根据被调节量的变化进行运算后,发出的使外部执行结构按其要求动作的指令,即整个调节器的输出。请注意与调整量yout(t)的差异。这两个概念完全不同,人们经常混淆这两个概念。
其实:你经常会看到公式“u(t)= KP[e(t)+1/ti∫e(t)dt+TD * de(t)/dt]”中的u(t)。
4输入偏差:输入偏差时调整量与设定值之差。
实际上:误差(t)=rin(t)-yout(t)。
P(比例):P是比例作用,简单来说就是输入偏差乘以一个系数。
现实:和kp一样,KP也一样。
I(积分):I是积分,简单来说就是对输入偏差进行积分。
现实:如ki。
d(积分):D是微分,简单来说就是输入偏差的微分运算。
现实:比如kd。
8 PID基本公式PID调节器参数整定过程一般来说是先将系统调整到纯比例作用,逐渐加强比例作用使系统产生等幅振荡,记录比例作用和振荡周期,然后将这个比例作用乘以0.6,适当延长积分作用。
KP = 0.6 *公里
KD= KP*π/4ω或KD= KP*tu/8
KI= KP*ω/π或KI= 2KP/tu
KP:比例控制参数;
KD:积分控制参数;
KI:微分控制参数;
Km:系统开始振荡时的比例值,通常称为临界比例值;
ω:等幅振荡的频率,tu为振荡周期。这里,tuω =2π,而不是tuω=1。学过傅里叶和拉普拉斯变换的同学应该明白这是为什么,这里就不深入讨论了。
9.单回路:单回路是只有一个PID的调节系统。
10级联:一个PID不够。串级就是将两个PID串联起来形成串级控制系统,也叫双环控制系统。在串级控制系统中,PID调节器可分为主调节器和辅助调节器。
在串级控制系统中,被调节量的PID称为主调门,其输出直接指导执行机构动作的PID称为副调门,主调门的控制输出进入副调门作为副调门的设定值。主调节器采用单回路PID调节器,辅助调节器采用外部调节器。
1积极效果
对于PID调节器来说,控制输出随着被调节量的增加而增加,随着被调节量的减少而减少,这就是所谓的PID正效应。
12负面影响
对于PID调节器来说,控制输出随着被调节量的增加而减小,随着被调节量的减少而增加,这就是所谓的PID负效应。
13动态偏差
在调节过程中,被调节量与设定值之间的偏差是随时变化的,两者之间的随时偏差称为动态偏差。
14静态偏差
调整趋于稳定后,调整量与设定值仍有偏差。静态偏差的消除是通过PID调节器的积分功能实现的。
15回电
调节器的调节功能表现为被调节量开始由上升变为下降,或者由下降变为上升趋势再变为回调。

你明白吗?