魏刚中学时就痴迷于数学。其中,最引人入胜的是那些他在中学时认为很深奥的数学内容。比如微积分和极限,欧几里德第五公设等等。但5次方程没有根式解,这是困扰卫岗时间最长的问题。感谢互联网和信息时代,魏刚有机会找到很多关于数学知识的视频。魏刚在对世界多位大师详细分析的基础上,对5次方程的无根解有了深刻的理解。

当然,由于伽罗瓦理论的深刻性,在没有根式解证明的情况下,魏钢还不能完全理解5次及以上方程的数理逻辑,但基本思路还是有的。数学学习给卫岗带来了很多快乐,也在卫岗引发了很多思考。快乐和思考应该是生活的重要组成部分。
也许是因为当时缺少素材,没有娱乐,卫刚才迷上了数学。如果今天的手机遍布全球,如果游戏克服了所有的情况,想要痴迷数学是非常困难的。这就给我们现代人提出了一个很严肃的问题:如果让今天的孩子爱上学习数学会怎么样?问题是如果数学成绩不好,孩子的未来会受到很大影响。毕竟我们生活在一个有很多考试门槛要过的社会,其中数学是最重要的一门。

其实为人父母是很矛盾的。一方面,似乎数学知识在自己的生活和工作中用处不大。另一方面,需要强调和孩子一起学习数学的重要性。真的没有什么好的方法可以突破这种心理障碍。唯一有效的办法可能就是家长多读一些与现代数学相关的有趣文章,慢慢培养一些关于数学的爱好,让孩子有底气学好数学。

这些都是题外话,现在我们回到伽罗瓦的理论。我们前面解释过什么叫没有根式解,决定5次及以上方程没有根式解是因为数。今天我们来讨论伽罗瓦证明的一些秘密。关于伽罗瓦定理证明的内容,目前市面上还没有科普书。有一本书《阿贝尔的证明》,算是比较有深度的作品。本书末尾的附录还列出了阿贝尔证明5次方程无根式解的细节,算是一本很有深度的科普书。但是,阿贝尔的证明还是太复杂了,一般人大概不会看那本书的附录。

魏钢在这里讲伽罗瓦理论更详细的内容,可以说是一个大胆的尝试。希望可以作为参考,有更多的科普作家给大家深度科普佳作。
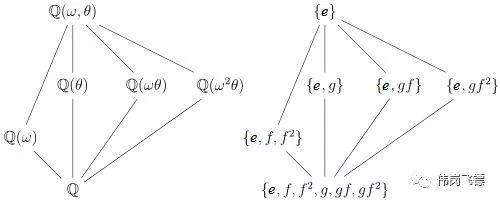
我们来看看课本上是怎么描述伽罗瓦定理的,上面说:域F上的不可约多项式f(x)=0有根解的充要条件是f(x)的分裂域是F的伽罗瓦群G=Gal(E/F)的可解群。
这么简单的一句话,却是天才数学家几千年努力的结果!伽罗瓦被证明已经过去200多年了,即使有了大学学历,我们仍然无法理解这个证明,可见数学进步的艰难。

我们遇到的第一个问题是定义域f,很多这方面的书直接把它定义为有理数域(数学上一般用大写q来表示,很奇怪,因为字母q好像和有理数没有关系,也不知道它的来历)。这也需要一点想象力。一般多项式的系数一定是有理数,所以多项式的系数一定在有理数域q内,关键是你怎么区分一个多项式和其他多项式?这时候就会出现分裂域。
其实多项式域F可以包含任意多项式,但是由于多项式方程的根不同(如果根相同,则为同一多项式),所以分裂域也不同,从而可以区分不同的多项式。这样,回答第一个问题,什么是域f,我们暂时认为是有理数域q。

不可约多项式,我们之前说过,就是不能在有理数域分解。稍微想一想就很好理解了。如果一个多项式是可约的,可以先做因式分解,再研究不可约部分。换句话说,任何多项式都可以通过研究不可约多项式来研究,其目的当然是为了简化研究。

之所以只研究不可约多项式,是因为后面的证明只对不可约多项式成立。如果是可约多项式,分裂域上可能会加有理数,这就意味着分裂域是有理数扩张域的定义被破坏了,至少有很多特例。

接下来要理解的是伽罗瓦群是什么。这个我们前面讲了一些,但是还没有触及问题的难点。为了便于理解,我们这样来描述伽罗瓦群的定义:在域Q上多项式的分裂域上(即把域Q上多项式的根相加形成一个扩张域),做一些自同构,把Q上的值(即所有有理数)映射到自己。这些自同构形成了分裂域E上的伽罗瓦群..

这里是思维能力的测试。也是理解伽罗瓦理论的一大难点。首先,什么是自同构?从定义上来说就是映射,就是让Q上的值(也就是所有有理值)映射到自身。这样的映射存在吗?理论上应该有很多方程可以使所有有理数在等号两边相等(即构造一个方程,使得当未知数是有理数时,方程两边相等)。要找一个具体的例子,魏钢想了半天也没想出来。关键是除了有理数,其他范畴的数都不能让这个等式两边相等。

在这里,我们要消除另一个误解,那就是我们认为自同构是一个虚无缥缈的东西。必须说明的是,我们讨论的是数学范围内的问题,所以即使自同构是抽象映射,也是数学概念。简单来说,自同构就是一些数学变换。至于具体的变换,因为群论不研究具体的计算,所以数学家没有列出具体的表达式。他们认为没有必要。你只需要承认这些转变是存在的。

在这个阶段,你肯定会有更大的疑惑,那就是即使你承认自同构的存在,这样的自同构不是有无穷多个吗?也就是说,你如何寻求这些抽象的变换?
贾华真是个天才,他构思出了求伽罗瓦群所有自同构的算法!(后来的数学家是否在伽罗瓦思想的基础上得到了伽罗瓦群中的自同构不得而知,但即使后来的数学家做到了这一点,也肯定是受到了伽罗瓦论文的启发,所以数学史书籍和教科书大多把功劳归于伽罗瓦)。

注意到伽罗瓦群在分裂域中求自同构,即在有理数域中加多项式方程根构成的域。伽罗瓦通过两点确定了所有的自同构(我们不能说伽罗瓦完全找到了所有的自同构。抽象代数就是这样训练我们的思维的。要跟上伽罗瓦的思路,就必须抛弃初等数学中形成的许多固定套路。)首先,构成伽罗瓦群的自同构将有理数映射到自身(这是伽罗瓦群自同构的定义);其次,这些自同构将多项式方程的根映射到其他根。

第一点似乎很明显,不用说。事实上,正是这个隐患决定了决定所有自同构的关键。第二个证明可以在课本上看到,也有点头疼。证明的关键点是将那些方程根的自同构映射带入多项式方程,可以转化为方程值的映射。因为根是使方程为零的数值,所以自同构是零的映射,反过来证明这些自同构映射后使方程为零。也就是说,构成伽罗瓦群的映射都是将多项式的根映射到其他根。这些内容有点绕,这也是学习抽象代数的特点,抽象推理需要思考和想象。

确定伽罗瓦群的自同构是多项式方程的根映射到其他根,然后根的对称性就出来了。这可能也是群论的一个本质,但是很难理解。
细心的同学朋友可能还记得,多项式方程的根在某种意义上是对称的。我们注意到复数根是共轭的。也就是说,根的实部相等,虚部之前的加号和减号都是根。这意味着在复平面上,两个轴遵循一个圆,并且是对称的和实的。即使是平方减2等于零的简单方程X,也有对称的正负根号2。

根的对称性决定了伽罗瓦群中自同构的一个根到另一个根的映射是一种旋转变换。数学家正是从这个结果得出伽罗瓦群其实同构于置换群的结论!或者伽罗瓦群同构于对称单群。对称性是五次和五次方程没有根式解的主要原因,它的意义原本隐藏在伽罗瓦群和对称群同构的命题中!

找出一个特定伽罗瓦群同构的精确对称群仍然是困难的。但我们可以简单描述一下基本思路。寻找的过程当然也需要自同构定义给出的条件,否则属于伽罗瓦群的元素的自同构映射可能是到其非对称根的根映射,进而无法找到伽罗瓦群的同构群。
一般一个对称群对应一些旋转和位置变换,寻找Galois群的同构对称群就是寻找与这些旋转和位置变换一致的变换。课本都很简单。只有非常细心和耐心的人才能理解推导过程,普通读者只需要知道结果就可以了。

抽象代数对抽象对象的精确分析和计算,给了我们很多值得深思的课题。同时要摒弃一切具体计算的思维模式,用新的套路学习数学,这不是每个人都能做到的。

如果能找出许多多项式的伽罗瓦群(或者准确地说,找出伽罗瓦群的同构对称群),可以说对伽罗瓦理论的理解前进了一大步。但是要理解伽罗瓦的证明,还有更深刻的数学知识。最难理解的是可解群。什么样的群是可解的?

群的可解性与群的子群和群的正规性有关。粗略地说,一个方程之所以没有根式解,是因为如果把有根式的数加到方程的分裂域上,这些数必然会使伽罗瓦群有子群,而这些子群必须满足正规性等条件,如果不满足这些条件,就不存在有根式的数。但是记住,多项式方程的根必须存在(这叫代数基本定理),我们不能把有根的数作为方程的解加到分裂域上,所以方程无根解。

这时候,问题来了。有没有无法求解的伽罗瓦群?这是当然的。事实上,大部分5次及以上的方程都同构于不可解的对称群。贾华还发现了不可解的伽罗瓦群对应的5次方程,从逻辑上证明了5次及以上方程没有根式解。

如果想理解伽罗瓦的证明,还有更多东西要学。至少你应该知道什么叫正常群体。这涉及到群论的全部知识,要讲很长时间。今天的空间也差不多。下一篇再说群论的具体知识。
文末,感谢朋友同学的鼓励和奖励!数学的知识很渊博,理解现代数学并不难。希望魏刚的文章带给我们思考和乐趣。