先举一个例子:
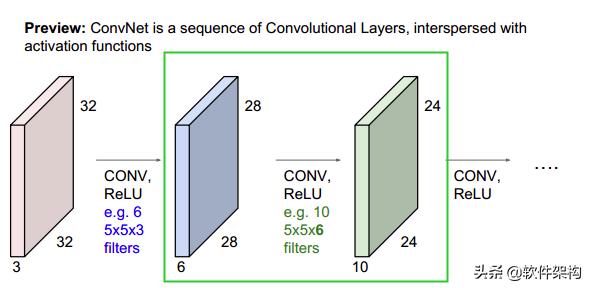
比如输入小编女朋友的图片,是一个32x32x3的图像,3表示RGB三通道,每个filter/kernel是5x5x3,一个卷积核产生一个feature map,下图中,有6个5x5x3的卷积核,故输出6个feature map(activation map),大小即为28x28x6。

其中28 的计算公式:
神经元个数: (32-5+1) * (32 -5 +1) = 28 * 28 个。也就是每一个feature map的大小就是28 * 28 。

实际上,在卷积过程中,输入层(Input)有多少个通道,卷积核(滤波器Filter)就要有多少个通道,但是卷积核的数量是任意的,卷积核的数量决定了卷积后 feature map 的通道数。
第一层(卷积层)的参数个数计算先整理以下此环境中对应的数据信息。
Filter个数:6
- 原始图像shape:32*32*3
- 卷积核大小为:5*5
- 一个卷积核的参数:5*5*3=75【3是input通道数,三个通道的权重并不共享。 所以对于以上的计算,三通道的参数数量应该还要乘以3。】
6个卷积核的参数总和:
75*6 + 6 = 450 + 6 = 456
weight * x + bias根据这个公式,即可算的最终的参数总额为:456
【其中weight 指一个卷积核的参数,x 指卷积核的个数,也就是输出通道数,bias 指偏置项,和卷积核的个数保持一致】
简单小结
卷积层的参数个数和图片的大小无关,它只和卷积核(Filter)的尺寸、深度以及当前层卷积核的个数有关。
CNN权值共享就是同一个Feature Map中神经元权值(weight)共享,该Feature Map中的所有神经元使用同一个权值。
第二层(卷积层)的参数个数计算这里忽略了池化层,池化过程只是图片大小发生了变化,深度没有发生变化。
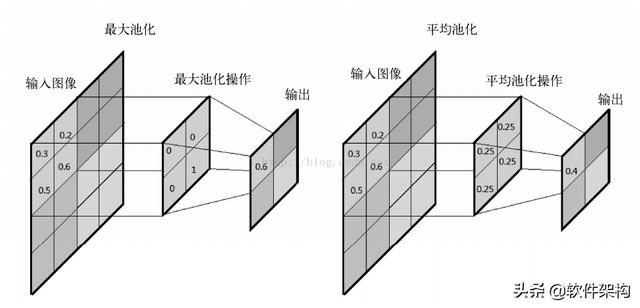
池化层:对输入的特征图进行压缩,一方面使特征图变小,简化网络计算复杂度;一方面进行特征压缩,提取主要特征。
下图中,第二层到第三层,其中每个卷积核大小为5x5x6,这里的6就是28x28x6中的6,两者需要相同,即每个卷积核的“层数”需要与输入的“层数”一致。
有几个卷积核,就输出几个feature map,下图中,与第二层作卷积的卷积核有10个,故输出的第三层有10个通道。
Filter个数:10

- 原始图像shape:28*28*6
- 卷积核大小为:5*5
- 一个卷积核的参数:5*5*6=150【是input通道数,6个通道的权重并不共享。 所以对于以上的计算,6通道的参数数量应该还要乘以6。】
10个卷积核的参数总和:
150*10 + 10 = 1510
卷积层中参数个数计算小结卷积核的个数=最终的feature map的个数
一个卷积核的参数大小=开始进行卷积的通道数×每个通道上进行卷积的二维卷积核的尺寸
合计参数的个数=卷积核个数×(一个卷积核的参数大小+1) 【其中+1 是偏置项Bias,和卷积核个数保持一致,也就是说偏置项 b 在同一个卷积核是共享的】

