这篇论文是为了“第三届数学文化征文比赛

从HPM的角度看等腰三角形的性质

课堂记录

作者:陈龙

工作编号: 058

1.创设情境，引入话题

老师:PPT展示以下图片。

图中的屋顶给了我们怎样的几何形象？

生:等腰三角形。

老师:我们再来看看这块古罗马墓碑。学生能猜出墓主的身份吗？

我听一些同学说，如果我们能翻译墓碑上的字母，我们就可能知道墓主人是谁。太好了！其实虽然我们看不懂他的墓志铭，但是有同学注意到这个墓碑的顶部很有特色吗？(学生在老师的指导下专注于墓碑顶部)

生1:我观察这个墓碑的顶部是等腰三角形和铅垂线的组合。

生2:我们可以猜测这个墓主人一定是从事几何和测量相关的工作。也许他生前是一位伟大的数学家。

老师:学生的观察和推理能力真强！据考证，这块墓碑的主人生前是一名土地测量员。想必他一定对自己的几何知识和土地测量员的身份深感自豪。所以，他把他的工具刻在了墓碑上。事实上，如果我们抽象出这个墓碑顶部的几何图形，我们就会得到右边的图形。这个图形由一个等腰三角形和一条垂在顶点的铅垂线组成。这是一种叫做水平仪的工具。这是一个非常古老的工具。在我国，我国古代勤劳智慧的劳动人民也掌握了它的工作原理，并应用于生产生活的实际。当工匠建造房屋时，他们可以用它来测量横梁是否水平。你知道原因吗？不懂？想知道关卡是怎么运作的吗？上完今天的课你就明白了！好了，我们继续今天的探索之旅，一起探索等腰三角形的本质吧！

老师:把题目写在黑板上:等腰三角形的性质

设计意图:从学生的实际生活和知识水平出发，感受生活中的等腰三角形，通过古罗马墓碑抽象出的水平仪提问，渗透数学文化，引起学生的好奇心，激发学生的好奇心和解决问题的兴趣。

二。探索新知识的实践操作

老师:按照下面的步骤，看看我们能得到什么样的几何。为什么？能解释一下原因吗？

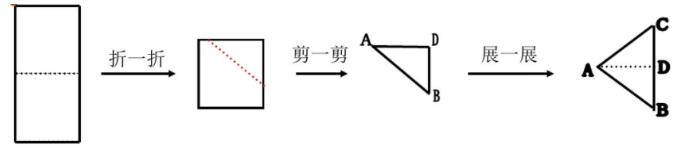
生:得到等腰三角形。

生:原因是根据等腰三角形的概念，等边的三角形叫等腰三角形。

师:相等的两条边叫腰，另一条边叫底边，两条腰之间的夹角叫顶角，底边和腰之间的夹角叫底角。

设计意图:让学生利用轴对称切割等腰三角形，复习等腰三角形的相关概念，为探索等腰三角形的性质做准备。

老师:仔细看自己剪的等腰三角形纸。你能找出这个等腰三角形有什么特征吗？

学生:独立思考(由老师巡回指导)。

师生活动:学生独立思考后，尝试总结自己剪的等腰三角形纸片的特点，并交流报告。如果学生找不到结论，或者结论总结不全面，教师在巡视时给出以下提示:将剪好的等腰三角形纸片沿折痕对折，找出重叠的线段和角度。

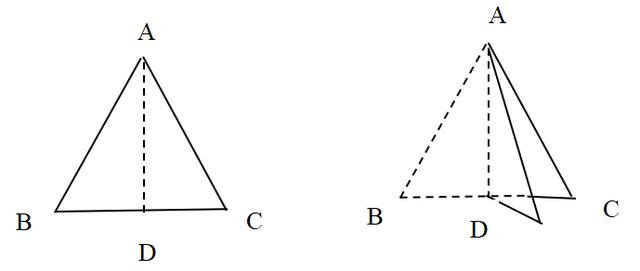
设计意图:让学生从一个等腰三角形入手，发现其特殊性。

老师:你们每个人剪的等腰三角形的纸片大小不一，形状也不一样。都有上面总结的特点吗？

师生活动:学生相互比较，分组合作交流，共同探索总结，完成下表。

性质一:等腰三角形的两个底角相等；

性质二:等腰三角形的顶角平分线，底边上的中线，底边上的高重合。

设计意图:通过感性材料，让学生在动手操作过程中发现等腰三角形的共同的、本质的特征，猜测和总结三角形的性质，在此过程中形成感性认识，重视知识形成的过程，培养学生自主探究的学习方法。

师:用实验操作的方法，我们发现并总结了等腰三角形的性质1和性质2。对于性质1，哪位同学能告诉我们这个命题的题目和结论是什么？

生:题目是:三角形是等腰三角形；结论:它的两个底角相等。

老师:你能画一个图形，用符号语言写出已知的和已验证的信息吗？

生:已知:如图，in △ABC，AB =AC..

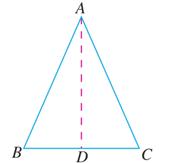
证明:∠ b = ∠ c。

老师:太好了！我们学过哪些证明角度相等的方法？

生:两条直线平行，同位置角相等，错角相等；都等着。

师:结合刚才的作图和操作(将等腰三角形纸对折)，你想用什么方法证明∠B=∠C？

学生:取底边中点D，连接AD，构造全等三角形。

生:我觉得可以作为底边的高度。根据“HL”也可以证明两个三角形全等。

生:我做了顶角的平分线。根据“SAS”可以证明两个三角形全等。

老师:三个学生的方法都是正确的。下面以底部中心线为例，请同学们谈谈证明的方法。

师生活动:学生可以独立完成。教师巡回，个别指导。

老师的示范。

已知:如图，in △ABC，AB=AC，BD = CD。

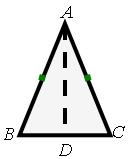
证明:∠B =∠C

证明:在△ABD和△ACD中

∴△Abd≔△ACD(SSS)。

∴∠B =∠C

老师:还有别的证明方法吗？

生:三种方法。

师生活动:学生板书表演(选择一种喜欢的方法)教师有意识地选择不同方法的学生上台表演。

设计意图:这里让学生经历一个完整的命题证明过程，在书面语言、符号语言、图形语言之间进行转换。我们可以从运算中找出添加辅助线的方法，体会到添加辅助线与解决问题的关联性。同时老师会在黑板上演示，在规范学生书写格式后让学生用各种方法证明，感觉不同的辅助线指向同一点。

师:这样，我们就证明了性质(等边等角)。

从上面全等三角形的证明过程中，你能得出什么结论？

健康:∠BAD=∠CAD，∠ADB=∠ADC=90。

师:以上三种证明方法中的辅助线有什么特点？

生:都是折痕AD。

老师:好！现在让我们一起来阅读大自然。

生:一起读书的品质

老师:你发现了什么？

生:原始的自然是自然的扩展！本质上都是一样的！证明自然，证明自然！

老师:你怎么理解“三合一”？

生:如果是等腰三角形顶角的平分线，那么这条线也是底边的中心线和底边的高度。

生:如果是等腰三角形底边的中心线，那么这条线也是顶角和底边高度的平分线。

生:如果是等腰三角形底边的高度，那么这条线也是底边的中线和顶角的平分线。

老师:很好！如何用几何语言表达:(学生回答，老师板书)

①∫AB = AC，BD=CD

∴AD平分AD⊥BC的BAC

②∫AB = AC，AD均分为∠BAC

∴BD=CD,AD⊥BC

③∵AB=AC,AD⊥BC

∴AD平分∠BAC，BD=CD

设计意图:引导学生发现等腰三角形的共同本质特征。并通过证明，进一步培养学生的抽象概括能力和初步的逻辑推理能力；如果学生真正理解了“三位一体”的含义，就会把“三位一体”分解成三个命题，体验等腰三角形性质2的本质。

三。回顾日历的历史，找到根

师生活动:老师PPT展示著名的等边等角历史证明法，学生欣赏品味。(以下是PPT演示，以欣赏为主。)

老师:你知道吗？等腰等角是欧几里得《几何原本》第一章的第五个命题:

原命题是:“在等腰三角形中，两个底角相等；而如果腰部向下延伸，那么底部以下的两个角是相等的。

如果用现代符号表示，这个命题的陈述和证明如图:

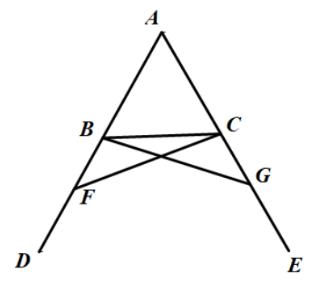
设ABC为等腰三角形，AB=AC，延伸AB，AC得到BD，CE，

那么∠ABC=∠ACB，∠CBD=∠CBE。

证明:取BD中任意一点F，切AE中AG=AF(命题3)，连接FC和GB。

AF = AG，AB=AC，∠FAG为公角。

∴△afc≌agb(4号提案)

∴FC=GB,∠ACF=ABG,∠AFC=∠AGB.

还有:AF=AG，AB=AC

∴BF=CG

∠∠AFC =∠AGB，FC=GB

△BFC≔△CGB(命题4)

∴∠FBC=∠GCB.∠BCF=∠CBG

还有≈ABG =∠ACF

∴∠ABC=∠ACB

老师:这个命题是欧几里得《几何原本》第一章的第五个命题，也就是全书的第五个命题。据说中世纪的时候，欧洲的数学水平很低。学生初读“原文”，学习第五个命题“等腰三角形的底角必相等”时，觉得很难。所以这个命题被嘲讽为“驴的桥”，意思是傻子都过不去的难关。也有人推测这个名字来源于欧几里德的制图，很像最简单的木桁架桥。

老师:除了欧几里得，历史上还有很多著名的学者研究过等腰等角。等腰等角还有很多其他证明。让我们来欣赏一下历史上那些大数学家的风采。

帕普斯法医学欣赏

帕普斯(约公元300-350年):古希腊数学家，公元4世纪。

证明了“等腰等角”，其证明方法别出心裁，把△ABC看成两个三角形，一个是△ABC，一个是折叠后的△ACB。

AB = AC，AC=AB，∠BAC=∠CAB，

∴△ABC≌△ACB(SAS)，

∴∠ABC=∠ACB。

欣赏普罗克拉斯的法医方法

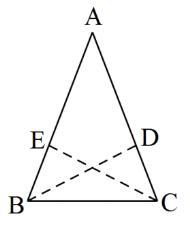
普罗克洛斯:(普罗克洛斯，公元410- 485年)公元5世纪。他还证明了“等边等角”(图2)。他的证明方法和欧几里得的类似，同样使用三角形同余的“角边”判断法。但普罗克拉斯并没有延伸腰部AB和AC，而是直接在腰部AB和AC上取E点和D点，使AE=AD，然后连接EC和DB。同样，他用“角边”两次证明三角形同余。

设计意图:了解数学史，渗透数学文化，感受数学课的人文精神和教育价值，从而激发学生的学习兴趣和热情。

四。运用新知识解决问题

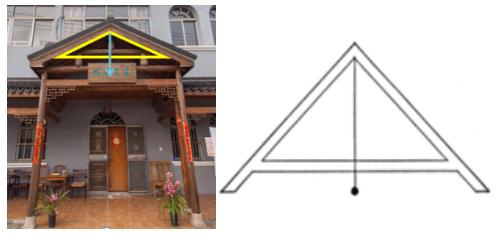
老师:现在，你能解释一下水平仪是如何帮助工匠测量横梁是否水平的吗？

当铅垂线通过底边中点时，横梁是水平的。

老师:为什么？推荐人是谁？

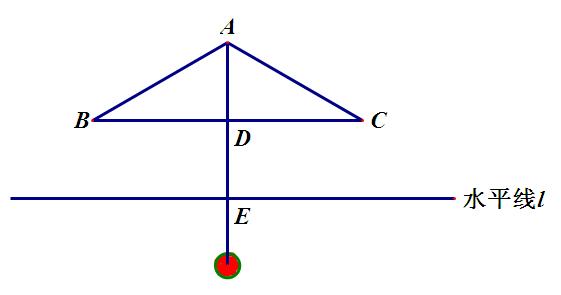
生:以横线为参照，我们可以从这个实际问题中抽象出上图所示的数学模型。所以这个问题转化为证明BC平行于直线l，利用等腰三角形的性质2，就做到了。

老师:太好了！水平仪是一个非常古老的物体。事实上，今天世界上许多地方仍在使用它。它的工作原理就是我们今天学到的等腰三角形的“三合一”。中国古代的劳动人民非常勤劳和聪明。

设计意图:学以致用，介绍历史中关卡的使用。一方面与课堂导入相呼应，另一方面让学生感受等腰三角形在现实生活中的应用，实现数学来源于生活，服务于生活的新课程理念。同时，感受中国古代劳动人民的智慧，增强他们的文化自信和民族自豪感。

五、课堂实践，能力提升

1.已知在△ABC中，AB=AC，∠ B = 80。求∠C和∠ a的度数。

老师:这里∠B是-？

生:△ABC的底角？

老师:你怎么知道？

健康状况:已知状况

生2:画个图，一看就知道。

学生独立完成。

变体训练:

(1)已知在等腰三角形△ABC，∠b = 80°中，求∠C和∠ a的度数。

老师:这个问题和上一个问题有什么区别？

生:没有告诉我们∠B是顶角还是底角，需要分类讨论。(让学生尝试独立完成，然后集体评论，并引导学生自己画图帮助理解。)

已知在等腰三角形△ABC，∠ b = 100，求∠C和∠ a的度数。

老师:这个问题需要讨论吗？为什么？

生:不会，因为底角不会超过90。

生:独立做。

总结:在等腰三角形中，如果知道任意一个角的度数，就可以求出另外两个。当已知条件中未明确给出的角为锐角，不知道是顶角还是底角时，需要分类讨论。

2.如图，AB=AC，AD是△ABC的中心线，∠ B = 50，则∠ bad =

生:用三线合一，可以看到AD还是高于△ABC的。

设计意图:通过典型例题的变化，培养学生的发散思维，渗透分类讨论的数学思想。教师可以通过适当的“导入”来启发学生积极“探究”，使师生双边活动“共振”，和谐发展。

六。总结、扩展和改进

老师:同学们，这节课你们收获了什么？

生:等腰三角形的性质是:“等边等角”和“三条线合一”

生2:我觉得数学知识往往是通过动手操作获得的。

生3:知道数学史上那么多数学家对等腰三角形的探索和证明，真是大开眼界！

生4:我也知道液位计是怎么工作的，感觉棒极了！

……

七。分级经营，整合与提升

(1)a组:

1.在等腰三角形△ABC，∠a = 60°中，求∠C和∠ b的度数。

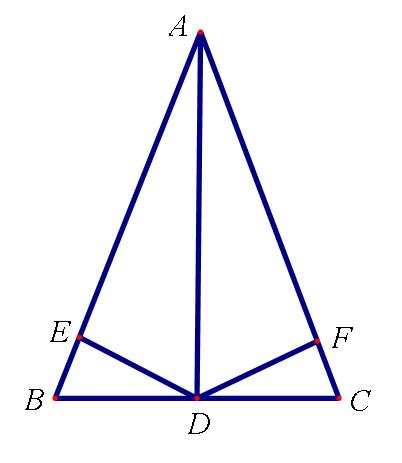
2.如图，在△ABC中，AB=AC，AD⊥BC在d点，过d点如同DE⊥AB在e点，DF⊥AC在f点，若BE=3，求CF的长度

设计意图:1、2都是简单的应用，以便更好的理解属性。同时为下一节研究等边三角形做铺垫。(全班都要完成。)

b组

1.如图，在△ABC中，AB = AC = 5，AD等于∠BAC，而AD = 4，BC = 6。如果点P在边AC上移动，求BP的最小值。

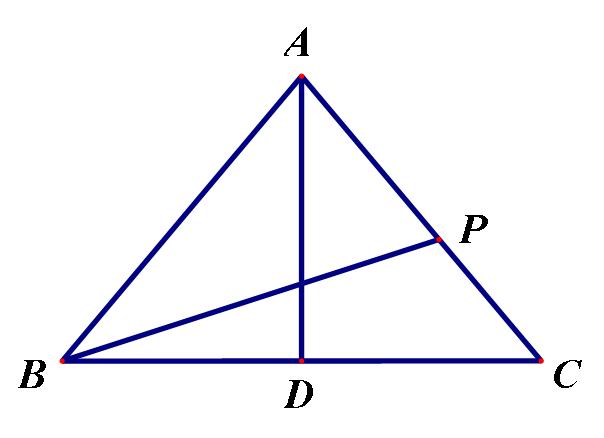
设计意图:简单的应用性质2，在一组的基础上稍作改进和扩展，帮助学生。(供中级以上水平的学生选择。)

c组。变体:

证明:底边到两腰距离相等的点在顶角平分线所在的直线上。

设计意图:这个班的同学对文字证明题比较陌生，对三种语言之间的转换不是很精通。所以设置这个问题，既巩固了文字证明题的解题方法，又拓展和丰富了练习，供有空余时间的同学选择。

相关链接> & gt

相聚于网络，相知于数学，相约于征文——第三届数学文化征文活动通知

第三届数学文化征文大赛评委简介

第二届数学文化征文比赛通知

首届数学文化征文活动征文集

发表的文章> & gt

01莱布尼茨，二进制和伏羲卦

02.美学视野下的数学教学——读《数学的美与理》的思考

03数学基础与黎曼猜想——读《数学简史:决定论的消失》有感

04数学与文化并重，知识与兴趣同行——对“数数”教学的思考

05数学是一门多维艺术——读《数学家的眼睛》有感

06从骰子到阿尔法狗:有趣的概率

07中学数学分类思维的教学与发展

看门人的秘密

09探索数学文化，启迪数学美——以割圆为例

00数学史视角下的高中数学教学思考

01如何阅读《几何原本》

02两座相映成趣的数学桥梁。

013 HPM视角下的数学概念教学——“平面直角坐标系”的教学设计

04极限定义新讲座:动态定义与静态定义

05掌握思维方法自主提高数学素养——读后感让知识自然生长

06读北京大学张教授《数学的源流》有感

中国古代数学对“一带一路”沿线国家的影响

08数学阅读锦上添花，实践成果引领几处新征程。

09提高概率教学质量的几点思考

00.回顾过去，建构新知，论证，产生巧思——三角形中线定理探究

01读《学好数学不难》有感触

02.体验经典证明渗透数学文化——以勾股定理教学(第一课)为例

03数学文化数学——融入数学文化的中考试题分析及启示

04善用数学文化，智慧数学课堂，优化育人方式

05基于数学文化的高中数学教学实践与研究

06数学之美——读《数学文化中的美育渗透》有感

07.“去分母”解一元一次方程的教学设计

08海伦公式

09《镜花缘》中的数学“缘”

00基于认知发展的数学理解教学——数学教学心理学读后感

031做一个有文化的数学教师——读《数学教育中的数学文化》有感

02扎根下来，追求成长

03.利用阅读之星解决中考文化试题的策略研究——以2021年福建和北京中考试题为例

2021中考04传统文化试题

05数学文化阅读教程——圆周率的历史

06年初中课堂渗透数学文化的思考——读张齐华老师《用文化滋润数学课堂》有感

07对丰富多彩的数学观和数学史的思考

38张小折纸，大有历史——可写入教材的“一刀一剪”最精准的五角星折法

2009年新高考改革背景下数学文化情境试题的调查研究——兼评2020年高考数学文化试题

00谈如何解决问题指导教学

01如何将数学文化渗透到正常的课堂教学中——读顾亚龙专著《用文学把人变成人》有感

02中学教材中的数学文化与中考命题分析

03初中数学教学中渗透民族文化自信

04初中数学教学中数学文化的渗透策略

第二章探索图形的规律——用火柴杆记录数学文化课堂

小学数学课堂教学中数学文化的渗透

07核心素养视角下的数学活动实施策略研究

08数学史视角下的初中数学教学思考——读《数学文化漫谈》有感

09读《张奠宙数学教育随想》的几点体会

00.读浙江大学蔡天新教授《数学的传说》有感

051 HPM视角下的一元二次方程概念教学实录及设计分析

02探索“1”单元下的直觉模型——读《测量:献给数学的情歌》有感

03数字是现实与想象的结合——读《测量:献给数学的情歌》后的想象

基于数学美的04小学数学命题设计

05“饮马将军”的前世

06“数学文化”答题活动的题目设计

07走近杨辉的秘密三角教学设计

07《走近杨辉的秘密三角》课堂实录

07走近杨辉的秘密三角的教学反思