文艺复兴时期17世纪著名数学家、哲学家笛卡尔《几何学》提出了虚数的概念，用i表示。当时的观念认为这是真实不存在的数字。后来发现虚数可对应平面上的纵轴，与对应平面上横轴的实数同样真实。人们一般认为虚数只是数学家的玩具（数学工具），并无现实意义，但最近一项研究表明虚数可能是有实际的物理意义。

在丹·布朗（Dan Brown）2003年的畅销悬疑惊悚小说《达芬奇密码》中，书中的主人公罗伯特·兰登（Robert Langdon）和密码学家索菲·奈芙（Sophie Neveu）之间有一点巧妙的应答，她在书中表达了对“信仰中包含奇迹般的事件”的宗教信徒的价值的怀疑。她冷笑道：“看来他们的真实是假的。”

兰登笑着说：“这些想法就像数学密码学家相信虚数‘i’能帮助他们破解密码一样。”

对于我们这些不懂数学的人来说，兰登的笑话有点令人费解。当他说一个数是虚数时，他到底在说什么？这怎么可能呢？

虚数（imaginary number）就是-1的平方根。

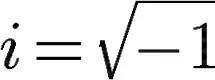
虚数到底是什么？它有什么用？

虚数是数学中的一种东西，最早是在15世纪和16世纪被发现的，用来解决某些令人困惑的方程。虽然最初被认为是一种数学把戏，但在此后的几个世纪里，它们被视为一种以复杂的方式将世界概念化的工具。如今，它们在从电子工程到量子力学等领域都很有用。

人们发明虚数的原因和发明负数的原因是一样的。如果透支信用卡去买东西，但没有足够的钱来支付，我们的银行账户就会出现负余额。

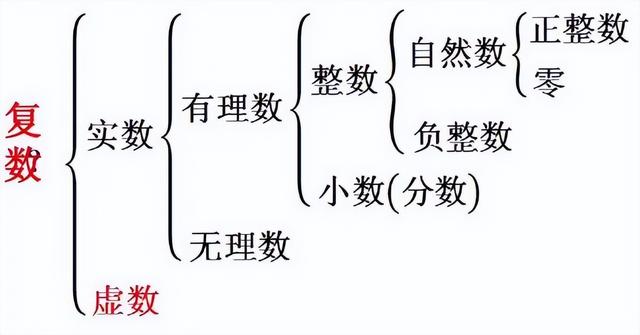
另一种看待负数的方法，这稍后会派上用场，是想象在城市附近散步。如果你从我们的目的地向相反的方向拐错了弯。比方说，向南走了5个街区，而你本来应该向北走，你就可以把它想象成向北走了5个负的街区。通过发明负数，它可以扩展你的数学世界，使你能够谈论以前很难的事情。

虚数和复数，也就是包含虚数成分的数字，是这种创造性思维的另一个例子。如果我问你，9的平方根是多少？这很简单，对吧？答案是3。尽管它也可以是- 3，因为两个负数相乘得到的结果是正的。但是-1的平方根是多少？有没有一个数，乘上它自己，得到-1 ？在某种程度上，没有这样的数字。

但笛卡尔想出了一个聪明的方法来解决这个问题。发明一个等于-1的平方根的数字，给它起个名字：i。高斯系统地使用了i这个符号，并主张用数偶（a、b）来表示a+bi，称为复数，虚数才逐步得以通行。

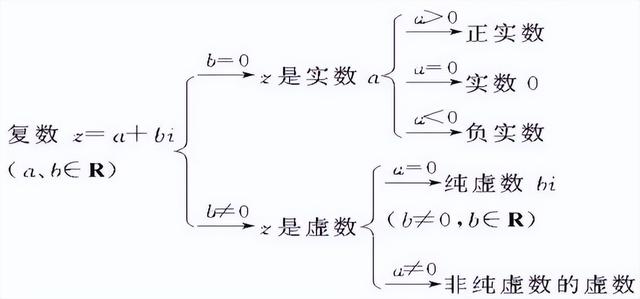
一旦想出了虚数的概念，数学家们就会发现他们可以用它做一些很酷的事情。像x²+1=0这样最简单的二次方程，在实数范围内没有解，而在复数范围，它可以有解了。

虚数闯进数的领域时，人们对它的实际用处一无所知，在实际生活中似乎没有用复数来表达的量，因此在很长一段时间里，人们对它产生过种种怀疑和误解。笛卡尔称“虚数”的本意就是指它是虚假的imaginary；

莱布尼兹则认为：“虚数是美妙而奇异的神灵隐蔽所，它几乎是既存在又不存在的两栖物。”

欧拉尽管在许多地方用了虚数，但又说：“一切形如,√-1，√-2的数学式子都是不可能有的，想象的数，因为它们所表示的是负数的平方根。对于这类数，我们只能断言，它们既不是什么都不是，也不比什么都不是多些什么，更不比什么都不是少些什么，它们纯属虚幻。”关联阅读：欧拉上帝公式：包括数学中最基本的常量e、i、π，哲学重要的0和1

挪威测量学家维塞尔提出把复数（a+bi）用平面上的点来表示。后来高斯又提出了复平面的概念，终于使复数有了立足之地，也为复数的应用开辟了道路。复数一般用来表示向量（有方向的量），这在水利学、地图学、航空学中的应用十分广泛，虚数越来越显示出其丰富的内容。

1843年，威廉·罗文·汉密尔顿（William Rowan Hamilton）将平面中的虚数轴的概念扩展到四元数想象的四维空间，其中三个维与复数域中的虚数相似。

随着多项式环的商环的发展，假想数的概念变得更加显着，但是也可以找到其他虚数，例如具有+1的平方的tessarines的j。

19世纪初，数学家们发现了另一种理解虚数的方法，即把虚数看作平面上的点。当我们把数字想象成直线上的点，然后加上第二个维度时，那个平面上的点就是虚数。

首先，假设有一根数轴，上面有两个反向的点：+1和-1。

这根数轴的正向部分，可以绕原点旋转。显然，逆时针旋转180度，+1就会变成-1。

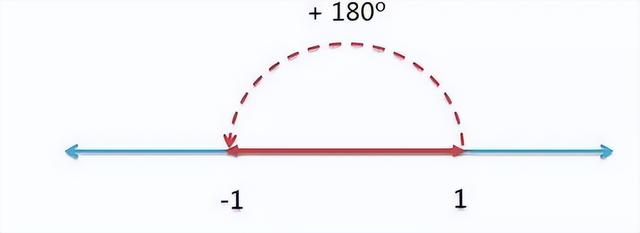
这相当于两次逆时针旋转90度。

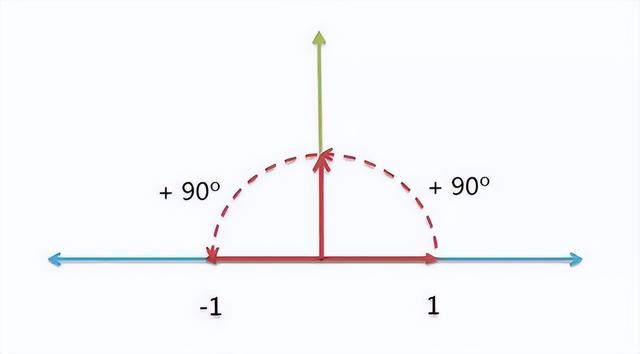
因此，我们可以得到下面的关系式：

(+1) * (逆时针旋转90度) * (逆时针旋转90度) = (-1)

如果把+1消去，这个式子就变为：

(逆时针旋转90度)^2 = (-1)

将"逆时针旋转90度"记为 i ：

i^2 = (-1)

这个式子很眼熟，它就是虚数的定义公式。

所以，我们可以知道，虚数 i 就是逆时针旋转90度，i 不是一个数，而是一个旋转量。

但是你不能把-1的平方根放在X轴上，这是行不通的。但是，如果你创建了一个垂直于X的Y轴，你就有地方放它了。

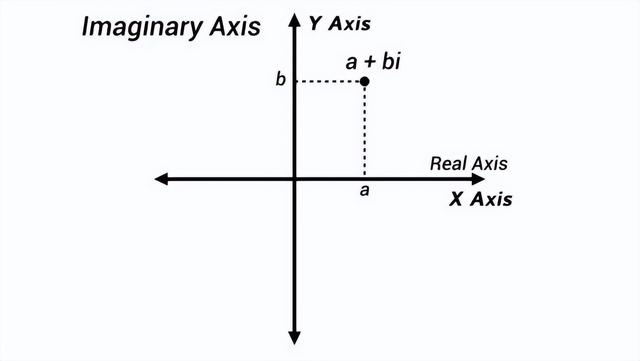
当你考虑虚数时，Y轴是有用的，因为你不能把根号-1放在X轴上。

既然 i 表示旋转量，我们就可以用 i ，表示任何实数的旋转状态。

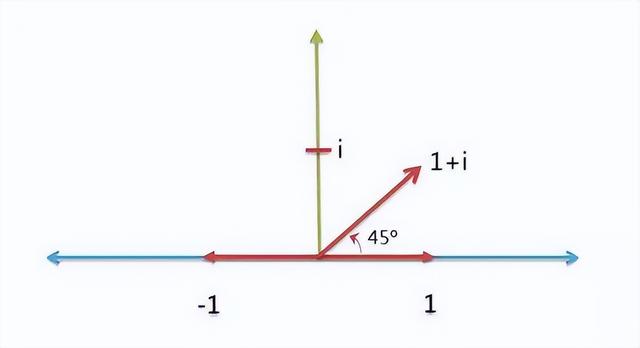
将实数轴看作横轴，虚数轴看作纵轴，就构成了一个二维平面。旋转到某一个角度的任何正实数，必然唯一对应这个平面中的某个点。

只要确定横坐标和纵坐标，比如( 1 , i )，就可以确定某个实数的旋转量（45度）。

数学家用一种特殊的表示方法，表示这个二维坐标：用 + 号把横坐标和纵坐标连接起来。比如，把 ( 1 , i ) 表示成 1 + i 。这种表示方法就叫做复数（complex number），其中 1 称为实数部，i 称为虚数部。

为什么要把二维坐标表示成这样呢，下一节告诉你原因。

虚数的作用：加法

虚数的引入，大大方便了涉及到旋转的计算。

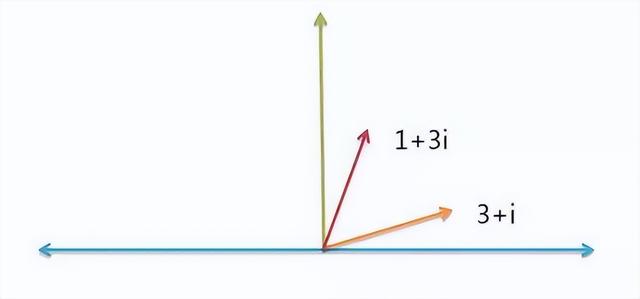
比如，物理学需要计算"力的合成"。假定一个力是 3 + i ，另一个力是 1 + 3i ，请问它们的合成力是多少？

根据"平行四边形法则"，你马上得到，合成力就是 ( 3 + i ) + ( 1 + 3i ) = ( 4 + 4i )。

虚数的作用：乘法

如果涉及到旋转角度的改变，处理起来更方便。

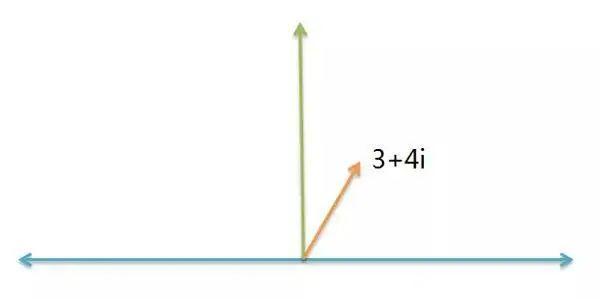
比如，一条船的航向是 3 + 4i 。

如果该船的航向，逆时针增加45度，请问新航向是多少？

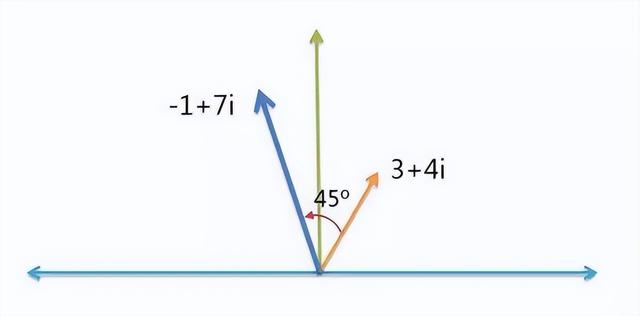
45度的航向就是 1 + i 。计算新航向，只要把这两个航向 3 + 4i 与 1 + i 相乘就可以了

( 3 + 4i ) * ( 1 + i ) = ( -1 + 7i )

所以，该船的新航向是 -1 + 7i 。

如果航向逆时针增加90度，就更简单了。因为90度的航向就是 i ，所以新航向等于：

( 3 + 4i ) * i = ( -4 + 3i )

这就是虚数乘法的意义：改变旋转角度。

复变分析

得到是欧拉公式

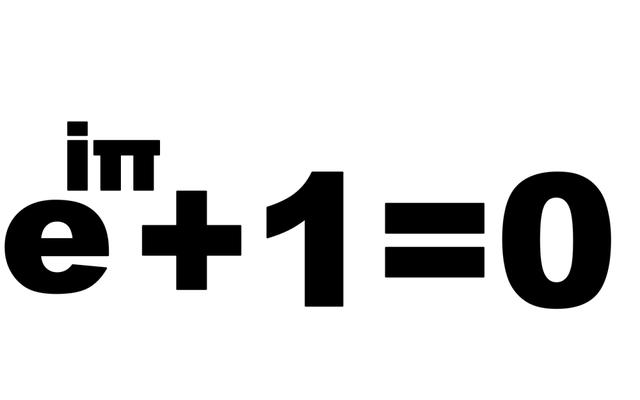
虽然虚数似乎只是一群数字，使人眼花缭乱，但它们实际上是非常有用的，对于世界上某些重要的现代技术发达的计算而言，如计算飞机机翼的气流，从阻力或找出流失能量结合在一个电力系统振荡。小说虚构人物的罗伯特·兰登提到它们也用于密码学时，他可不是在逗我们。

带虚分量的复数在理论物理中也很有用。由于它们与三角函数的关系，它们在描述，例如，周期函数时很有用。这些是波动方程的解，所以我们用复数来描述各种波，比如电磁波。因此，和数学一样，物理中的复杂微积分是简化计算的极其有用的工具。

复数在量子力学中也有作用，量子力学是一种在原子和亚原子粒子尺度上描述自然行为的理论。在量子力学中，‘i’明确地出现在Schrödinger的方程中。

量子系统的状态可以用它的波函数来描述。作为薛定谔方程的解，这个波函数是某些状态的叠加，叠加中出现的数字是复杂的。例如，量子物理中的干涉现象可以很容易地用复数来描述。

为了从根本上描述物质，虚数被证明是必不可少的。它们似乎融入了量子力学的结构，后者是描述分子、原子和亚原子粒子领域的基础理论。最近的两项新实验表明，遵循量子物理学规则的理论需要虚数来描述现实世界。

虚数经常作为数学工具出现在方程式中，以使计算更容易。但是我们可以实际测量的，关于世界的一切都是用实数来描述的，我们也习惯于正常的、非虚的数字。尽管虚数出现在理论中，但所有可测的量是实数。

虚数 i 是薛定谔方程必不可少的常数，量子力学必须包含虚数。量子理论对复数的使用令薛定谔（Erwin Schrödinger）感到不安。虚数在量子力学中都被视为一种方便的辅助工具，但到底是不是必要的还存疑。

部分物理学家试图仅使用实数来构建量子理论，而使用称为「实数量子力学」的版本来避免使用虚数。但是如果没有对这些理论进行实验测试，我们无法得知虚数在量子物理学中是否真的必要，或者只是一种有用的计算工具。

一种称为贝尔测量（Bell test）的实验解决了一个不同的量子难题，证明量子力学确实需要粒子之间的奇怪量子联系，也就是量子纠缠。

贝尔实验由英国物理学家约翰贝尔提出（不是发明电话的亚历山大贝尔）。

要了解标准量子理论和类似实数理论之间的区别，你可以思考限制在两个不同位置上的电子。在量子理论中，电子可以处于两个位置的「叠加」中——既不在这个位置，也不是在另一个位置，被观测到在哪只看概率。这种叠加被表示为包含两个维度的抽象空间中的一个点。

但这不是普通的空间，也不容易想象。抽象空间中的每个维度都通过一个复数与现实世界中的一个位置相关联，该复数可用于计算在该位置找到电子的概率。随着电子的状态随时间变化，该点在抽象空间中移动。

具有两个真实维度的类比空间不足以捕捉该电子可以表现出的所有现象，因为它无法编码两个位置的所有可能叠加。然而，具有四个真实维度的空间能够完整指出电子行为的全部范围。这个事实可以概括为：任何单个量子系统的量子物理学都可以在一个真实空间中完全表示，该真实空间的维度数恰好是其抽象空间的两倍。

维也纳量子光学和信息研究所的理论物理学家 Miguel Navascués 和来自奥地利、西班牙和瑞士等国家的科学家在 12 月 15 日发表于《自然》杂志的论文《Quantum theory based on real numbers can be experimentally falsified》中制定了一项实验计划。该论文的一作是量子信息科学的理论物理学家 Marc-Olivier Renou。

论文链接：https://www.nature.com/articles/s41586-021-04160-4

在实验计划中，研究人员将从两个不同的来源发送成对的纠缠粒子给三个不同的人，根据传统的物理术语命名为 Alice、Bob 和 Charlie。Alice 接收到一个粒子，并且可以使用她选择的各种设置对其进行测量，Charlie 也这样做。Bob 接收到两个粒子并执行一种特殊类型的测量来纠缠 Alice 和 Charlie 接收到的粒子。

没有虚数的实数量子理论将预测与标准量子物理学不同的结果，从而使实验能够区分哪个是正确的。

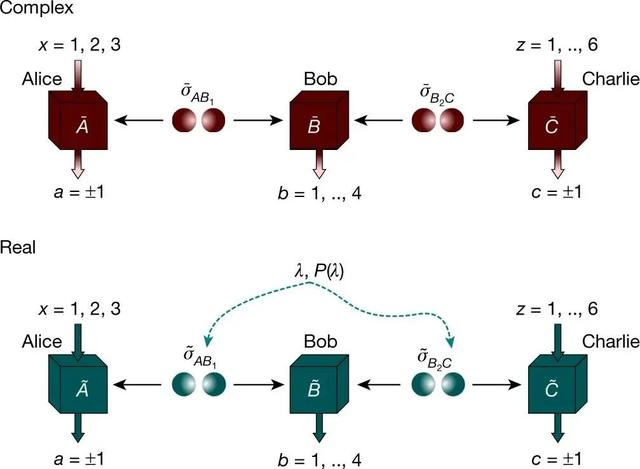
分离实数量子理论和复数量子理论的网络场景。

中科大潘建伟团队&南科大范靖云团队分别独立通过实验验证了虚数的必要性。结果则是

仅用实数不能描述标准量子力学的实验结果。

两篇论文同天发表在物理顶刊物理评论快报上。

△中科大论文

△南科大学论文

用超导量子、光量子分别验证Navascués论文。

中科大团队使用的自研的超导量子线路完成了这个实验。

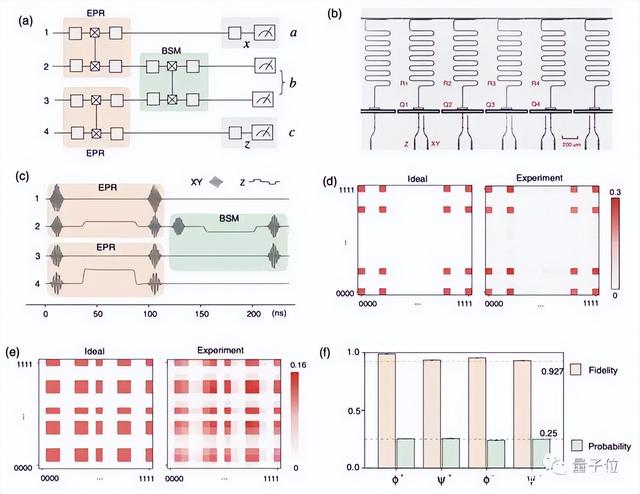
实验结果8.09，超过实数形式7.66的界限43个标准差（标准差为0.01）。

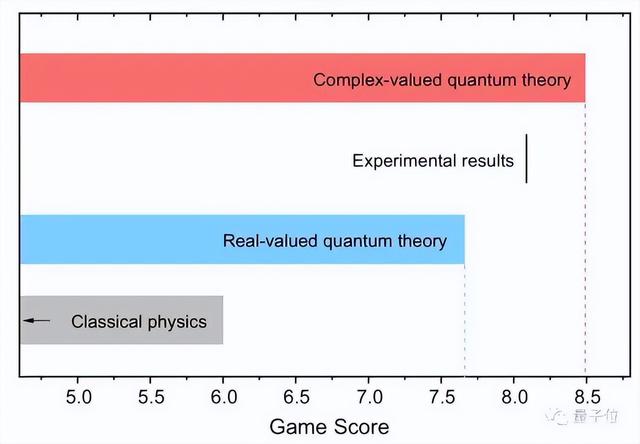
南科大团队采用了另一种思路，以光量子方法也完成了这个实验。

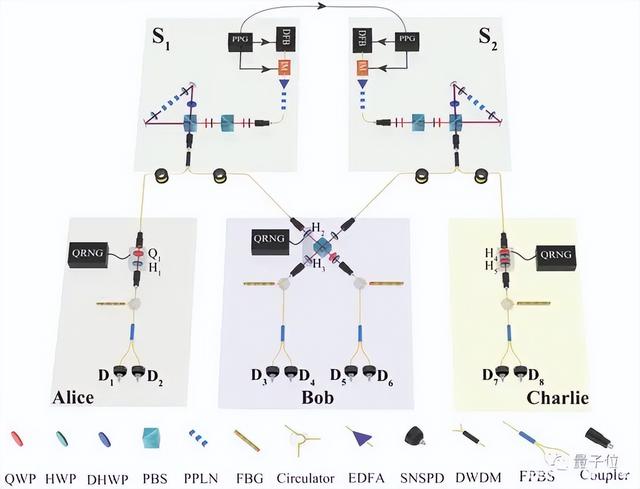
完整的贝尔态测量在线性光学系统中被证明是不可能的，因此论文中提出了部分贝尔态测量做替代。

实验结果也超出了实数形式界限4.7个标准差，同样支持了标准量子力学不能抛掉虚数的观点。

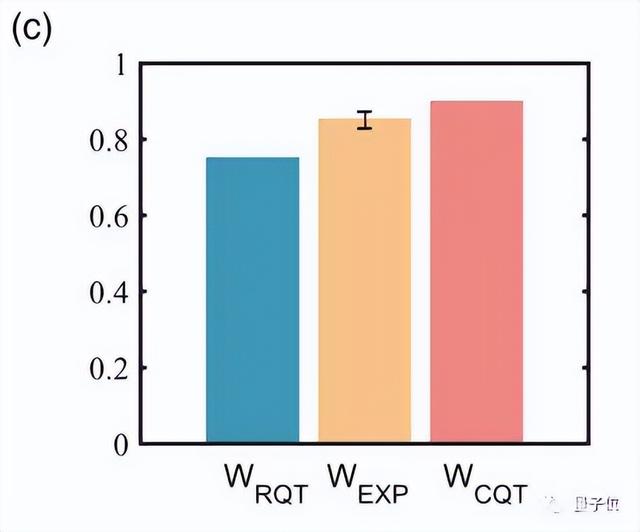
该实验证明了实数无法完整描述标准量子力学，确立了复数的客观实在性。随着量子力学理论的发展，复数逐渐表现出某种直觉上的不可排除性。理论上，作为量子力学基石的薛定谔方程和海森堡对易关系其本身就是依赖于复数写出的。而在实验中，人们直接测量到了波函数的实部与虚部。这说明复数可能不是一个主观引入的计算符号，而是可以实验检测的物理实在。

参考：量子位、机器之心