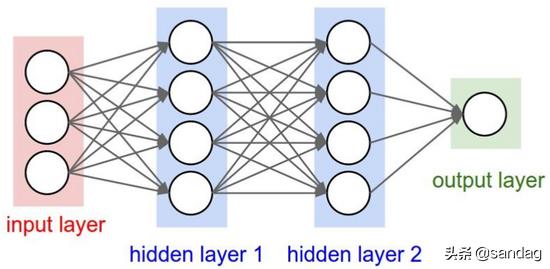
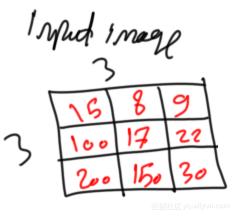
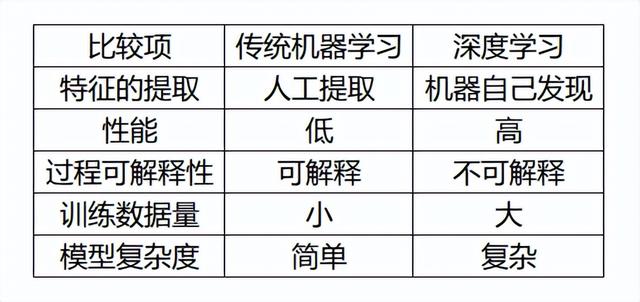
什么是深度学习
简单说,深度学习就是包含多个隐含层的多层感知机,通过组合底层特征,形成更为抽象的高层表示,用以描述被识别对象的高级属性类别或特征。能自生成数据的中间表示,是深度学习区别于其他机器学习算法的独门绝技。所以深度学习总结成:通过加深网络,提取数据深层次特征。
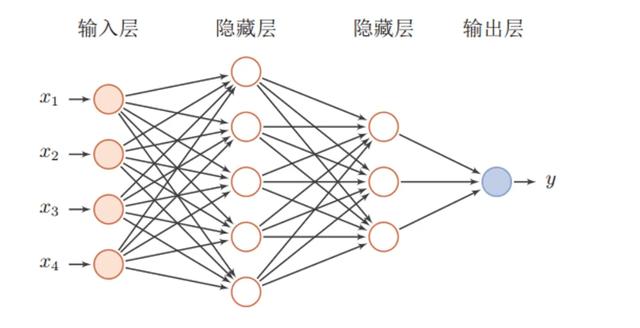
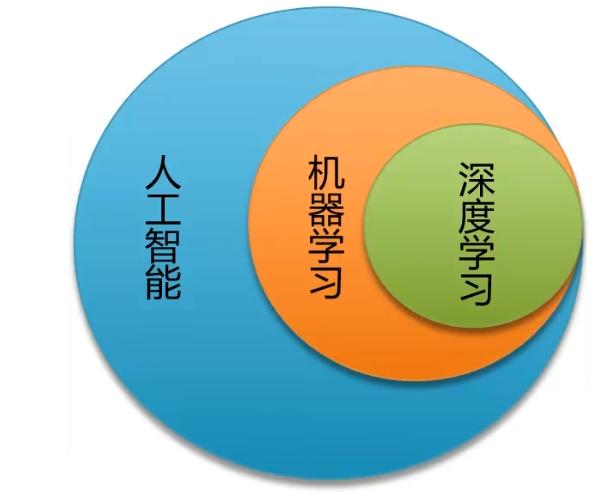
可以认为深度学习是机器学习的高级阶段。
深度学习的特点:
有点:
- 性能更加的优异
- 不需要特征工程
- 在大数据样本下有更好的性能
- 能解决某些传统机器学习无法解决的问题
缺点:
- 小数据样本性能不如机器学习
- 模型复杂
- 过程不可解释
感知机与神经网络
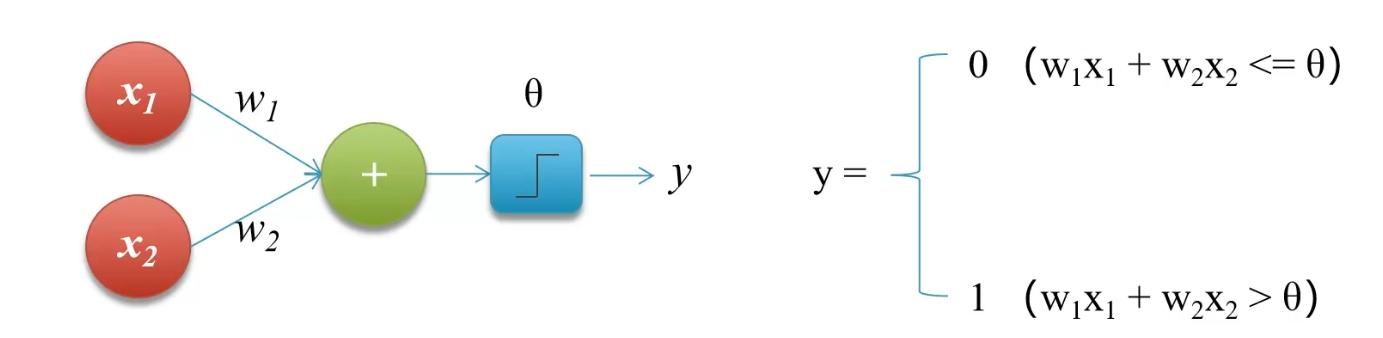
感知机,又称为神经元,是神经网络的起源算法,1958年由康奈尔大学心理学教授弗兰克·罗森布拉特提出,可以接收多个输入信号,产生一个输出信号。
感知机的功能:
- 实现逻辑运算,包括逻辑AND,逻辑OR
- 可以实现自我学习
- 组成神经网络
- 多层感知机可以实现异或问题
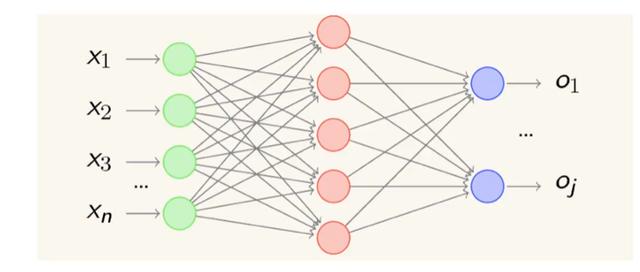
神经网络,感知机由于结构简单,功能有限,所以可以将若干个感知机连在一起,形成一个超级网络结构,结构称为多层前馈神经网络,前馈是指前一层的输出作为后一层的输入的逻辑结构,每一层神经元仅与下一层的神经元全连接,但在同一层之内,神经元彼此不连接,而且跨层之间的神经元,彼此不相连。
神经网络的功能理论基础,通用近似定理,对于任意复杂度的连续波莱尔可测函数,仅仅需要一个隐含层,只要这个隐含层包括足够多的神经元,前馈神经网络使用挤压函数作为激活函数,就可以以任意精度来近似模拟。如果想增加精度,单纯依靠增加神经元的数目即可实现。
激活函数,是指将输入信号的总和转换为输出信号函数被称为激活函数。激活函数将多层感知机输出转换为非线性,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
如果一个多层网络,使用练习函数作为激活函数的多层网络,称之为神经网络,否则称为多层感知机,所以激活函数是区别多层感知机和神经网络的一句。
常用激活函数
阶跃函数是一种特殊的连续时间函数,是一个从0调到1 的过程

sigmoid函数也叫Logistic函数,用于隐层神经元输出,取值范围(0,1),可以将一个实数映射到(0,1)区间,用于做二分类。
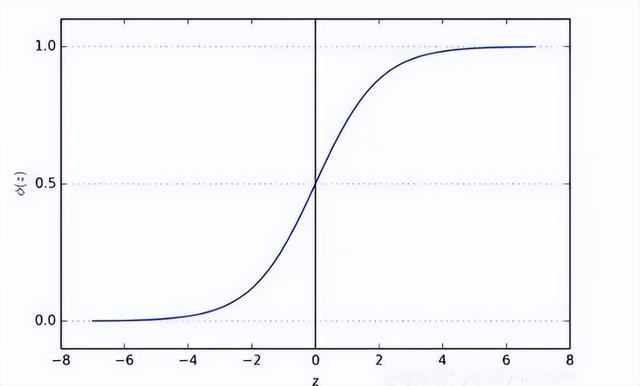
优点是平滑易求导,缺点就是激活函数计算量大,反向传播求导误差梯度时,求导涉及除法,反向传播时,容易出现梯度消失的情况。
双曲正切函数,缺点与sigmoid函数类似,容易梯度消失。
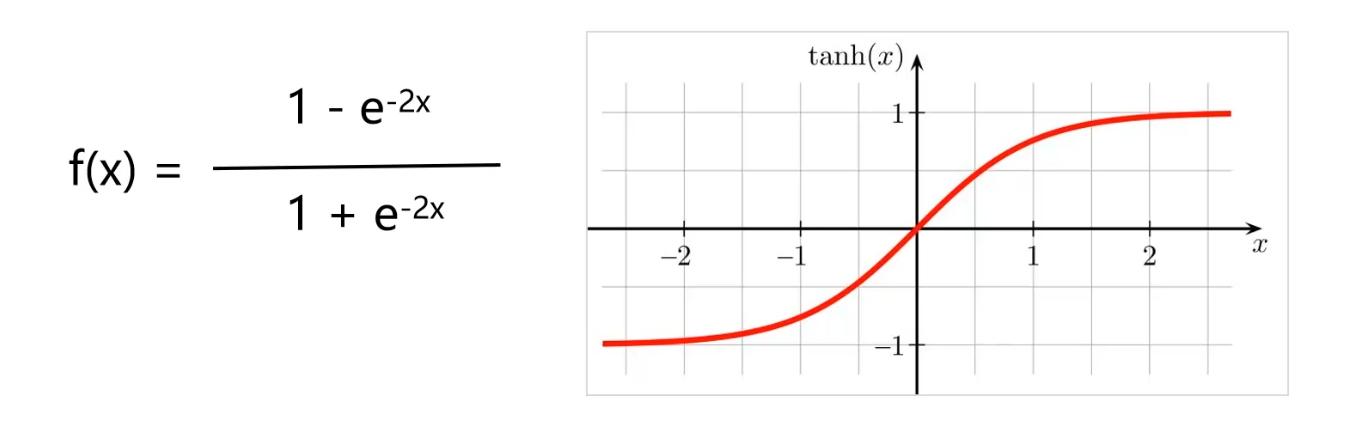
ReLu,修正线性单元,优点,更加有效率的梯度下降及反向传播,避免了梯度爆炸和梯度消失的问题,且计算过程简单。
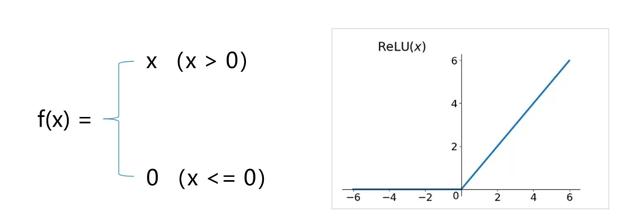
Softmax函数,将输入的值转换为0到1之间的相对概率,所有的公开加起来刚好等于1,一般用于分类器的最后一层。
损失函数与梯度下降

损失函数的作用,度量决策函数与实际值之间的差异。
作为模型性能的参考,损失函数越小,说明输出预测和实际结果之间的差值就越小,说明模型越好,学习过程中,就是不断通过训练数据进行预测,不断调整预测输出与实际输出差异,使的琐事值最小。
常用损失函数
均方误差损失函数,是回归问题的常用损失函数,预测值与目标值之间差值的平方和。
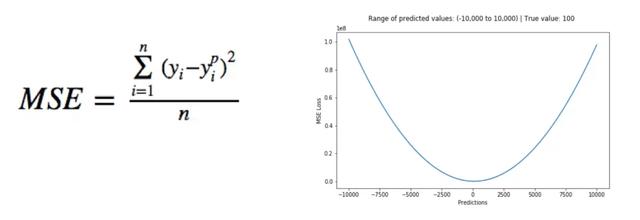
交叉熵,是信息论中的一个重要概念,主要用于度量两个概率分布间的差异性信息,机器学习中用来作为分类问题的损失函数。
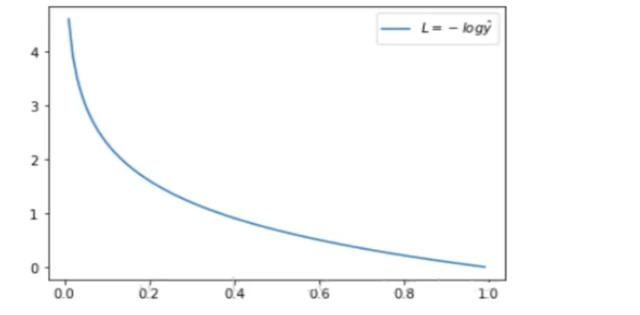
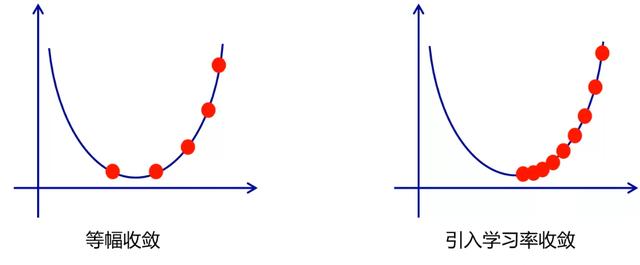
学习率,在梯度下降的过程中,每次都按照相同的步幅收敛可能错过极值点,所以每次在之前的步幅下减小一定的比例,这个比例称之为学习率。
批量梯度下降:批量梯度下降是最原始的形式,它是指在每一次迭代时使用所有的样本进行梯度更新。
优点:一次迭代是对所有样本进行计算,此时利用矩阵进行操作,实现了并行。有全数据集确定方向能够更好地代表样本总体,从而更准确地朝向极值所造方向。当目标函数为凸函数时,BGD一定能够得到全局最优。
缺点,当样本数目m很大时,每迭代一步需要对所有样本计算,训练过程会慢。
随机梯度下降,每次迭代使用一个样本来对参数进行更新,使得训练速度加快。
优点:由于不是在全部训练数据上的损失函数,而是在美丽的现代中,随机优化某一条训练数据上的损失函数,这样每一轮参数的更新速度打打加快。
缺点:准确度下降,由于即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线性收敛。可能很惨收敛到局部最优,由于单个样本不能代办全体样本的趋势。不易于并行的实现。
而综合以上两者的优缺点的是小批量梯度下降法。
卷积神经网络,针对全连接网络的局限做出的修正,加入了卷积层,池化层。卷积运算可以提取局部特征,起到对输入数据的平滑处理。
卷积神经网络通常由多个卷积层,激活层,池化层及全连接层组成。


卷积层,通过卷积运算,达到降维处理和提取特征的目的。
激活层,将前一层的线性输出,通过非线性的激活函数进行处理,用以模拟任意函数,从而增强网络的表征能力。
池化层,也称为采样层,下采样层,目的是缩小高、长方向上e空间运算,以降低计算量,提高泛化能力。池化层的主要特征,没有要学习的参数,通道值不发生变化,对微小的位置变化具有鲁棒性。
全连接层,这个网络相当于多层感知机,在整个卷积神经网络中起到分类器的作用。通过前面多个卷积-激活-池化的处理,待处理数据的特性已有显著性提高,一方面输入数据味道下降到可用传统的前馈全连接网络处理了,另一方面此时的全连接层输入的数据已经得到提纯,分类品质提高。