各位同学最近可能都在学习或复习正弦定理和余弦定理，应该知道正弦定理和余弦定理本质是在描述一般三角形的边角关系。已知△ABC，角A,B,C的对边分别为a,b,c，则正弦定理和余弦定理的内容表示如下：

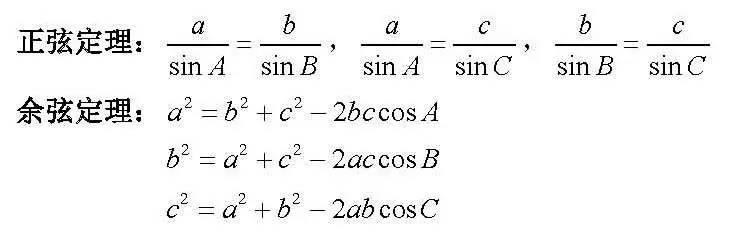
如果认为三条边和三个角是三角形的基本元素，那么正弦定理和余弦定理都是在刻画这6个基本元素中4个元素的某种等量关系。正弦定理刻画的是两边和两角的情形，余弦定理刻画的是三边和一角的情形，可能有同学会问，那么一边和三角的情形呢，因为含有一条边和三个角的情形只有以下三种：a,A,B,C，b,A,B,C，c,A,B,C，但是我们知道如果已知三角形的三个角，是无法求出任何一条边来，也就是说一边和三角的等量关系根本就不存在。

不难理解，要解三角形，首先得保证三角形能够确定，有以下几类：

①已知三边；

②已知两边和其中一边所对的角，可能会出现两解；

③已知两边和它们的夹角；

④已知两角和任意一条边。

为了方便计算，老师在教学过程中通常会强调利用正弦定理解三角形需要已知一组对边和对角，所以②④两类可以利用正弦定理来解，而①③两类可以利用余弦定理来解，这样可能部分同学会认为正弦定理和余弦定理是两个独立的定理，实际上它们之间的关系是等价的，只不过它们描述的角度是不一样的，因此理论上讲所有的解三角形问题都是可以同时利用正弦定理和余弦定理来解决。

下面笔者先给出正弦定理与余弦定理的等价证明过程：

篇幅有限，这里詹老师就不展开介绍正弦定理和余弦定理具体如何应用。可以看出，虽然理论上可以同时用正弦定理和余弦定理解三角形，但不同类型的问题利用它们来解决确实有运算量上的差异，因此各位同学在学习过程中还是要多积累使用正弦定理和余弦定理的经验，多体会正弦定理和余弦定理的应用特点。

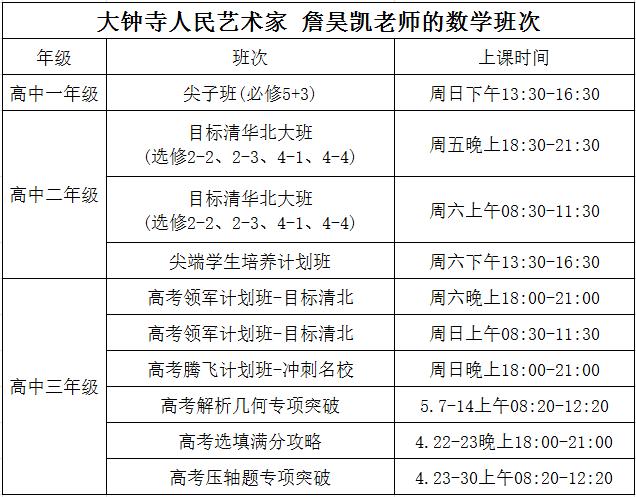
詹昊凯老师，学而思培优全职老师，02年至今有十四年高中数学教学经验，理科大牛，高考数学148，2004全国大学数学建模竞赛甲组一等奖。数学科班出身，知识功底深厚，有非常强大的逻辑思维能力与运算速度，责任心强，教学经验丰富，讲课思路清晰，了解不同层次的学生需求，能胜任各种班型教学。教学中非常注重学生的数学思维训练，善于幽默又不乏深刻，能极大提升学生学习数学兴趣，增强课堂学习体验，数学成绩提高明显，至今考入清华北大数十人，是一位有教育思想热爱研究的数学教师，相信没有不好的学生，只有不称职的教师。