达尔文的“进化论”可能是古往今来所有生物学理论中最著名、最有影响力的。在达尔文看来,所有物种的发展都必须遵循自然选择,所有物种都有一个共同的祖先。

俗话说,这么有影响力的理论,自然会遭到很多人的反对。时至今日,仍有很多人在质疑进化论的正确性。毕竟涉及到伦理问题,有争论很正常。
其实进化论是从《进化论》翻译过来的,更准确的翻译应该叫进化论。况且达尔文进入老年也没打算坚持自己的观点。他引用了一些反例来反对他年轻时提出的理论。例如,进化论无法解释眼睛等器官是如何被自然“选择”的。

直到一百年后的今天,众所周知的进化论本身并不只有达尔文的说法。比如孟德尔的遗传定律(达尔文自己也承认对这个理论一无所知),也被后来的进化论者抓住了。20世纪以后,随着卡尔·皮尔逊、罗纳德·费雪和约翰·斯密等英国科学家的发展,进化论逐渐引起了数学家和统计学家的注意,并成为应用数学中的一个重要研究对象。
那么今天的进化是什么样子的呢?下面小编带领读者看看现代进化生物学中一些有代表性的理论。
一、出发点——各种单物种模型
进化论是一个非常大的框架。为了研究一个物种真正是如何进化的,第一步是找出该物种的种群变化规律。为简单起见,我们先考虑一个物种的种群变化。
最简单的人口增长模型是只考虑生育率和死亡率的模型。可以用微分方程(如果考虑连续时间)或差分方程(如果考虑离散时间)来描述:

即使不懂微分或差分方程,也不难猜。如果出生率大于死亡率,这个种群就会继续繁衍,否则就会灭亡。其实上面微分方程的解是N(t) = C*exp[(b-d)t],说明这个物种的兴衰都是由(b-d)的正负决定的,正好验证了之前的猜想。正是因为这个原因,这个模型也被称为指数增长模型。
但这种简单的模型显然远远不能满足实际需求——要知道,一个物种是不能无限繁殖的,否则用不了多久地球就撑不住了,灭霸毁灭一半生命的野心也就实现了。因此,我们迫切需要一个更实用的模型Logistic增长模型(暂时忽略死亡率),用微分方程表示如下:
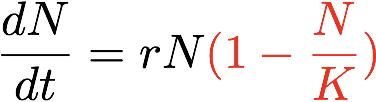
r是繁殖速度,K是种群的最大数量。例如,当k等于1时,种群以不同的繁殖速度变化如下:
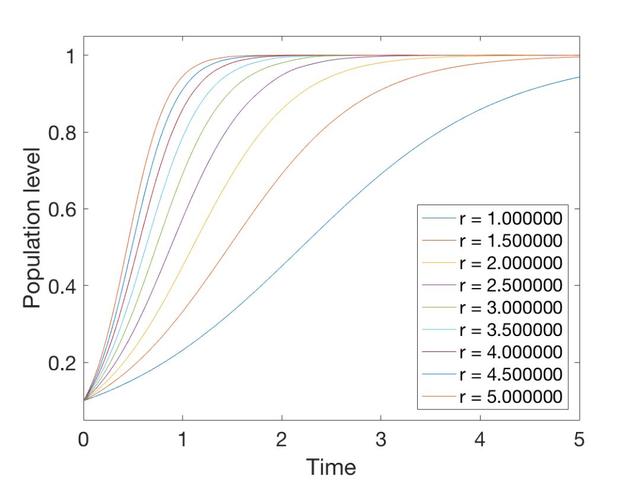
可见,无论繁殖多快,种群最终都会接近K值,但不会超过。一旦意外超过,必然会回到K值附近。
然而,逻辑增长模型并不一定反映真实情况。例如,美国生态学家瓦尔德尔·克莱德·阿利在研究金鱼的繁殖过程中发现,集中的种群有利于该物种的繁殖,如果种群密度过于稀疏,该物种很可能灭绝[1,2]。这个定律被后人称为Allee效应,它仍然可以用一个微分方程来表示:
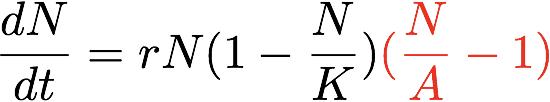
这里,A是一个待定参数,N代表物种密度,而不仅仅是总种群。所以从数学的角度来说,阿里效应无非是逻辑增长模型后面乘以一项。我们来看看一个物种在拥有不同初始数时的变化规律:
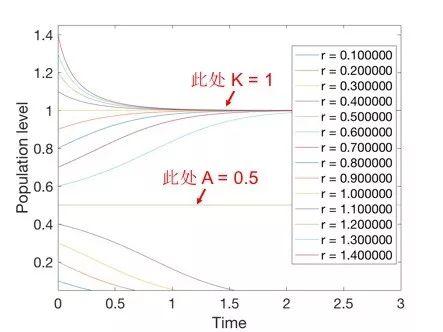
与逻辑增长模型不同的是,在Allie效应的作用下,低密度(n (0) < A)物种会走向灭绝。这就是为什么在保护和爱护动物的时候,建立自然保护区总是比在世界各地的动物园里放生或撒放更有效。
二、博弈论的引入——竞争就够了
在上一节中,我们讨论了单一种群的情况。但是生态圈是非常多元化的,一个物种不可能为所欲为。一方面,在食物链的作用下,捕食者和被捕食者的繁殖状态会有差异,但会有相关性;另一方面,捕食者和被捕食者群体之间会有竞争。例如,当只有一个捕食者和一个被捕食者时,可以用著名的Lotka-Volterra模型来描述:
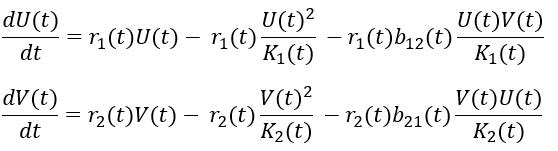
这个模型很受数学家欢迎,因为如果参数好,极限环是可以出现的。说白了,极限环描述的是捕食者与被捕食者数量之间的动态平衡,或者说是周期性的权衡。所以不要因为狼在童话中的形象不好就过度捕杀,猎物的数量会限制它们的成长。
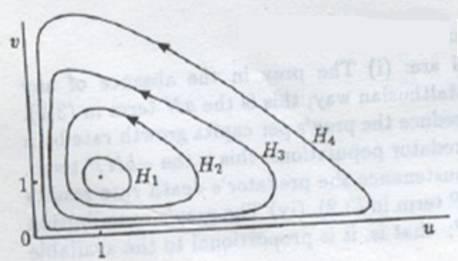
在介绍了与环境竞争和相互作用的机制之后,进化论者自然提出了一个新的问题——物种应该采取什么策略来:1。生存;2.好好生活,走上人生巅峰?这就需要用博弈论作为武器。
博弈论由冯·诺依曼创立,由约翰·纳西(电影《美丽心灵》的主角)发扬光大,并由进化生物学家约翰·梅纳德·斯密首先引入进化生物学领域。约翰·史密斯首次定义了进化稳定策略(ESS)的概念,作为进化化学中纳什均衡理论的一种类似。
史密斯考虑了一个简单的例子。假设有两个物种,鹰和鸽子,它们争夺同一个资源。我们知道,鹰是一种猛禽,生性好斗,人人都会打架。而鸽子天性温顺,打不过就跑。即使遇到势均力敌的对手,他们也更愿意平等分享资源,避免内斗。
根据上述假设,我们可以画出老鹰的“攻击性政策”和鸽子的“和谐政策”的收益矩阵:
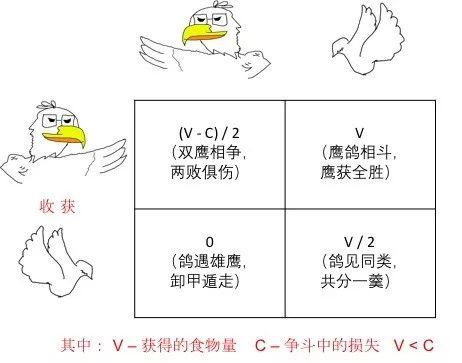

所谓一个生态系统的稳定进化策略,就是如何确定鹰和鸽的分配比例(即“攻击性政策”和“和谐性政策”),使整个自然系统达到平衡状态。根据小学数学,当鹰比是V/C,鸽比是(1-V/C)时,系统达到平衡状态。进一步,从大一数学知识(均衡矩阵的特征根都小于0)可知,这个策略的分布是稳定的,也就是说,当策略的比例分布失衡时,自然选择会使整个生态系统回归到上述比例。所谓“存在即合理”,无论是侵略性的还是和谐性的,都有其合理性,自然不会偏袒其中任何一方[3]。
有博弈论背景的读者可能会有一些体会——寻找一个生态系统的稳定进化策略,类似于寻找一个纳什均衡点(博弈各方相对稳定的状态)。其实两者之间也有一些微妙的区别。在纳什理论的框架下,一个纳什均衡点只是一个系统的均衡状态;但在进化过程中,这种状态要代代相传(具有稳定性到时间),这是一个动态的过程,所以稳定进化策略比纳什均衡点更严格。
三。结合遗传学的双剑
其实在达尔文提出进化论之前,法国生物学家拉马克就已经提出了“用回归理论”和“后天遗传”来解释器官的形成和长颈鹿脖子为什么那么长的理论。这个理论曾经影响很大。直到孟德尔的豌豆杂交实验出名后,进化生物学家才发现拉马克学说经不起孟德尔遗传学的检验,达尔文学说与孟德尔的结果并不矛盾。
虽然是植物学家,但孟德尔最大的成就是他敢于直接通过豌豆植株的宏观性状和简单的统计知识来猜测某些“看不见的基因”是遗传信息的载体,并第一次猜到了“基因”(等位基因,隐性显性基因)的基本结构。今天,我们知道基因本质上是DNA或RNA片段,但在孟德尔的时代,猜测这一点真的很有价值。
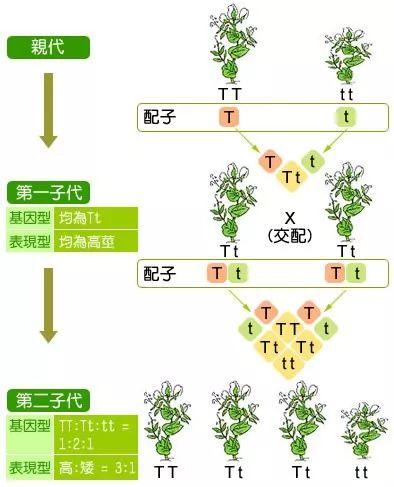
值得一提的是,遗传学的建立直接推动了现代数理统计的出现,因为在上面的图谱中,第二代基因型的比例并不是精确的1:2:1,而是随机的,而现代统计学的核心任务之一就是研究如何从随机数据中得到确定性的结果。另一方面,遗传学的基础使人们能够通过统计手段研究进化。例如,哈迪-温伯格定律:
事实上,这个定律的提出者之一哈代是20世纪初世界著名的数学家(现代分析学派的大师,华的研究生导师)。但是这个定律的数学背景很简单,就是(p+q) 2 = p 2+2pq+q 2。这个定律真正的过人之处在于其深刻的生物学意义,因为它告诉我们,在理想条件下,任何物种的后代基因型频率都是恒定的,因此生命的繁衍具有很强的稳定性。
这时候就有读者会质疑上面的模型——如果世代不变,生态系统的多样性在哪里?根本原因在于上述模型中极其苛刻的理想条件,例如,它假设个体物种的数量是无限的,个体之间的配对是完全随机的(癞蛤蟆吃天鹅肉的机会很大),等位基因与性别无关,物种不迁移,忽略基因突变和自然选择等等。
比Hardy-Weinberg模型更现实的叫做遗传漂变理论。在基因漂变理论的假设中,除了个体物种数量有限外,其他假设与哈迪-温伯格模型完全相同,但能产生与哈迪-温伯格定律完全不同的结论。
为了让读者更好地理解基因漂移理论的内涵,边肖进行了简单的模拟。假设一个物种的个体数为100,研究两个不同的等位基因A和B。假设这两个基因的初始频率为0.5,物种繁殖300代后,基因A和B的频率变化如下:
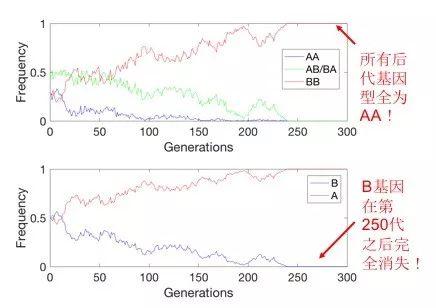
上述基因漂移模型的初始假设仍然很简单,自然选择、基因突变、线粒体遗传等诸多因素仍然没有考虑。如果在模型中加入这些因素,我们就要穿过狭窄的隧道,进入细胞甚至分子尺度才能一探究竟。

孟德尔认为基因是不可见的观点显然无法满足科学的需要。自20世纪50年代发现DNA以来,“基因”就与DNA密不可分,遗传学正式进入分子时代。
DNA最让人惊讶的是,所有的遗传信息完全包含在C、G、A、t四个碱基的排列组合中,那么DNA是如何控制生命的生长的呢?其实取决于氨基酸的合成,每三个碱基对应一个氨基酸。所以从理论上来说,只要能对一个物种的DNA进行测序,就能完全确定该物种的所有习性,并对该物种进行准确的分类!
物种分类起源于18世纪生物学家卡尔·林奈(Karl Linnaeus)等人的工作,然后人们常用系统发育树来描述生物分类的过程。但由于技术的限制,那个时代的分类方法主要依靠专家经验。生命科学进入分子时代后,逐渐利用不同物种DNA序列的异同绘制系统进化树。
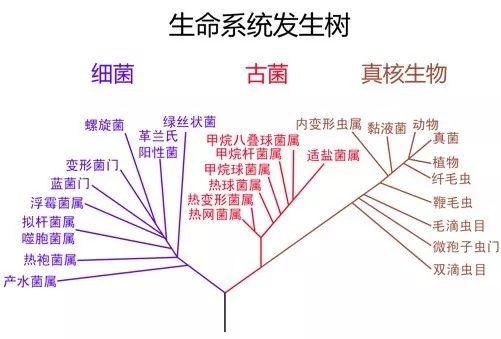
在最后一节中,我们知道基因漂移模型可以用来解释基因型消失的一个原因。但是从DNA的角度来看,并不能解释为什么生物的DNA(不仅仅是基因型)也会发生变化,因为基因漂移模型没有考虑到基因的突变。
那么如何研究基因突变对物种进化的印象呢?在数学家和统计学家看来,基因突变本质上是C、G、A、t四个碱基的随机变化,这个过程可以用马尔可夫过程(一种随机过程)来描述。马尔可夫过程本质上是从突变概率上分析不同的DNA序列是如何从同一DNA序列进化而来的,从而沿着系统发育树寻找不同物种之间的异同点(或距离)。
当然,不仅仅是进化生物学,上述计算方法在整个生物信息学领域都有广泛的应用,比如DNA和RNA测序等等。边肖将在以后继续谈论这些话题。
五.结论
在这篇文章中,边肖详细介绍了“进化论”的演变历史。我们可以看到,与100年前相比,今天的进化论在研究方法和深度上都有了很大的飞跃,达尔文进化论和孟德尔遗传学逐渐不再是学术研究的主流。虽然理论本身有瑕疵,但是他们提出的大方向是非常正确的,为后人的科学研究提供了很好的基础。
20世纪70年代,当人们对RNA和DNA越来越了解时,数学和统计学的研究方法被广泛应用于与基因工程相关的课题。但一方面,由于生命中存在大量的DNA和RNA片段,对大数据的分析和存储有很高的要求;另一方面,由于长链DNA的拓扑结构(甲基化、组蛋白诱导重塑等。)是非常复杂的,即使我们能够精确测量生命体中所有DNA和RNA的碱基序列,也远远不足以获得所有的遗传信息。
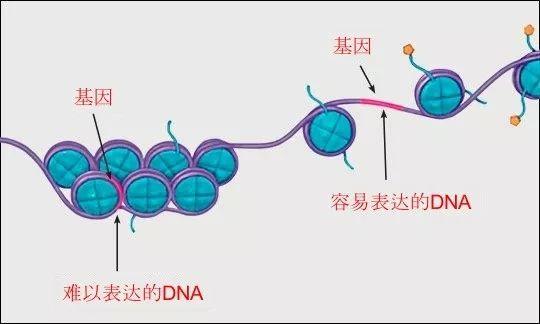
抛开生命科学本身,达尔文的进化论对其他学科的发展也有着非常重要的影响。比如在优化算法领域,有一类算法叫遗传算法,其本质是在已有答案的基础上,通过添加变异和链式交换机制,模拟一个“适者生存”的环境。与其他优化算法相比,它的优点是步骤简单,应用广泛,缺点是随机性太强,难以保证得到的答案一定是最优的。愿意亲自尝试遗传算法原理的读者可以登录http://boxcar2d.com/,用这个算法设计一辆能跑尽可能远,适应尽可能多地形的汽车。
最后,无论如何,进化论是一个非常伟大的理论。任何伟大的理论和学说都可能被批判,甚至可能有很多疏漏。但是,这些理论和学说对科学的发展有相当大的推动作用。随着生命科学和信息科学的飞速发展,新的颠覆性成果层出不穷。比如癌症领域,5年前的一篇学术论文可能已经过时了。因此,边肖建议对生命科学感兴趣的读者关注科学信息的前沿,而不是拘泥于一百年前的理论。反正欢迎读者提问。
参考资料:
[1]詹姆斯·d·默里。斯普林格,第三版(2007年12月8日)(经典教材)。
[2]阿利·WC,鲍文·E(1932)。"动物聚集的研究:金鱼对胶体银的大量保护& quot。实验动物学杂志。61 (2): 185–207.doi:10.1002/jez.1400610202。
[3]约瑟夫·霍夫鲍尔和卡尔·西格蒙德。剑桥大学出版社,1998年(经典教材)。
约翰·梅纳德·史密斯(1982)..ISBN 0-521-28884-3(经典著作)。
[5]朱克斯TH & amp康托尔河(1969年)。。芒罗·HN主编,《哺乳动物蛋白质代谢》,第21-132页,学术出版社,纽约。
[6]顾X,李W (1992)。。分子系统发育和进化。1 (3): 211–214.
转载内容仅代表作者观点。
不代表中国科学院物理研究所的立场。
如需转载,请联系原微信官方账号
来源:科普最前沿
原标题:进化论发展到什么程度了?
编辑:牧羊鱼