1471年,德国数学家米勒向诺德尔教授提出了如下十分有趣的问题:在地球表面的什么部位,一根垂直的悬杆呈现最长?即在什么部位,视角最大?最大视角问题是数学史上100个著名的极值问题中第一个极值问题而引人注目,因为德国数学家米勒曾提出这类问题,因此最大视角问题又称之为“米勒问题”,一般的米勒问题如下:

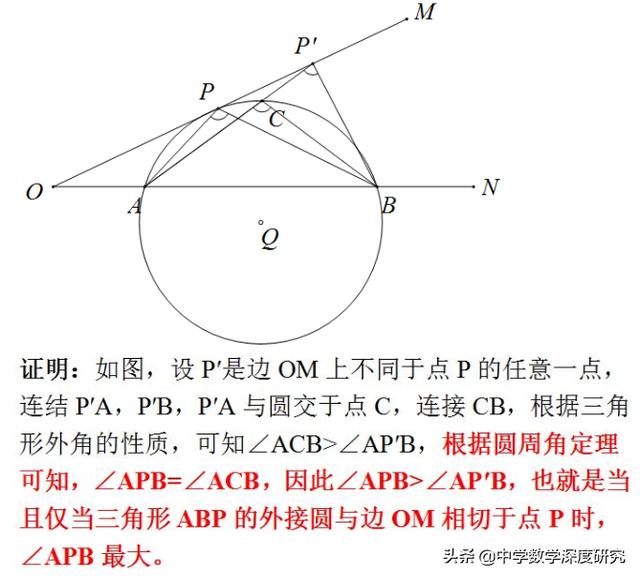

最大张角问题在数学竞赛、历届中考和模拟考试中频频亮相,常常以平面几何和实际应用为背景进行考查。若能从题设中挖出隐含其中的米勒问题模型,并能直接运用米勒定理解题,这将会突破思维瓶颈、大大减少运算量、降低思维难度、缩短解题长度,从而使问题顺利解决。否则这类问题将成为考生的一道难题甚至一筹莫展,即使解出也费时化力。
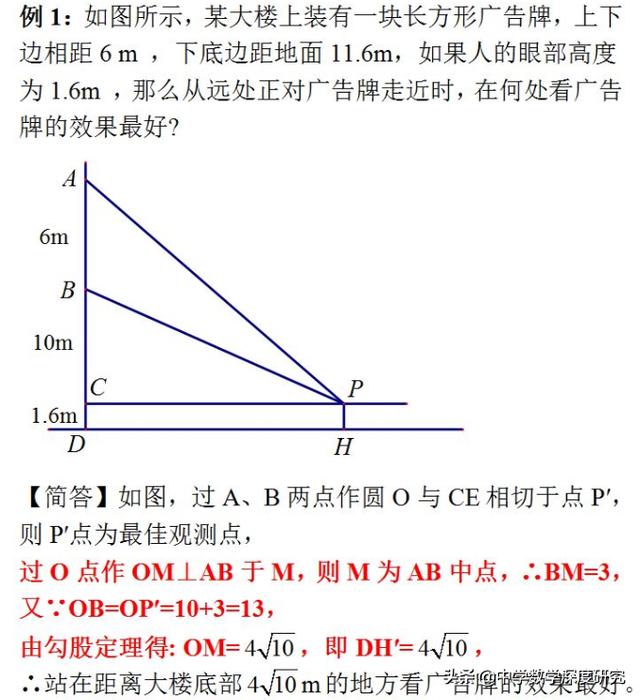
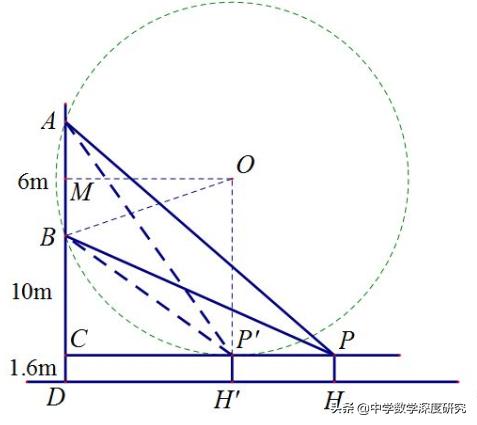


例3:如图,在每一个四边形ABCD中,均有AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12,在边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时cos∠BPC的值;若不存在,请说明理由.
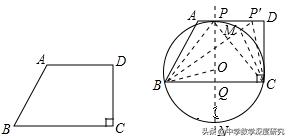
【解析】如图1所示,存在点P,使得cos∠BPC的值最小,作BC的中垂线PQ交BC于点Q,交AD于点P,连接BP,CP,作△BPC的外接圆O,圆O与直线PQ交于点N,则PB=PC,圆心O在PN上,根据AD与BC平行,得到圆O与AD相切,根据PQ=DC,判断得到PQ大于BQ,可得出圆心O在BC上方,在AD上任取一点P′,连接P′B,P′C,P′B交圆O于点M,连接MC,可得∠BPC=∠BMC≥∠BP′C,即∠BPC最大,cos∠BPC的值最小,连接OB,求出cos∠BPC=cos∠BOQ=OQ/OB=1/7,则此时cos∠BPC的值为1/7.
例4:(2019•雁塔区校级模拟)
问题背景:
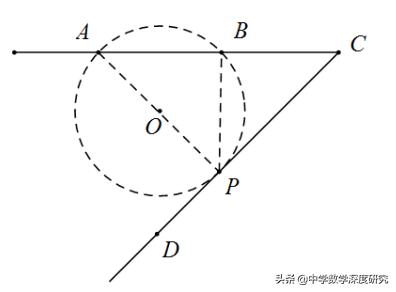
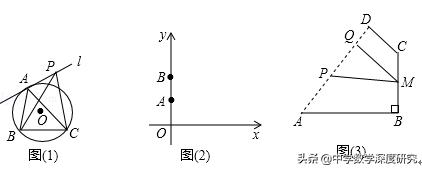
如图(1),△ABC内接于⊙O,过点A作⊙O的切线l,在l上任取一个不同于点A的点P,连接PB、PC,比较∠BPC与∠BAC的大小,并说明理由.

问题解决:
如图(2),在平面直角坐标系中,A(0,2)、B(0,4),在x轴正半轴上是否存在一点P,使得sin∠APB最大?若存在,请求出点P的坐标;若不存在,请说明理由.
问题应用:
如图(3),四边形ABCD是一个工厂中间的空地,其中AB边是一个宽为156米的加工车间(即AB=156米),BC边是一幢宽为96米的办公楼(即BC=96米),且AB与BC互相垂直,CD边是一面围墙,在办公楼BC的正中间安装有一摄像头M(即M为BC的中点)现想在办公楼对面的AD边上建一个宽为72米的车库PQ(即PQ=72米),使得摄像头M能监控到整个车库,其中AD长为180米,且AD与AB的夹角满足sinA=4/5,是否存在这样的车库位置,使得摄像头的监控效果最好(即∠PMQ最大)?若存在,请求出此时的AP长及sin∠PMQ的值;若不存在,请说明理由.
【解析】(1)如图(1),设BP与⊙O交点为D,连接CD
∵∠BAC=∠BDC,∠BDC>∠BPC,∴∠BAC>∠BPC.
(2)如图(2),过A,B两点作⊙C与x轴相切于点P,连接BC,CP
∵A(0,2)、B(0,4),∴点C纵坐标为3,
设点C坐标为(x,3),
∵⊙C与x轴相切于点P,∴CP⊥x轴,∴CP=3.
∵BC=CP=3,
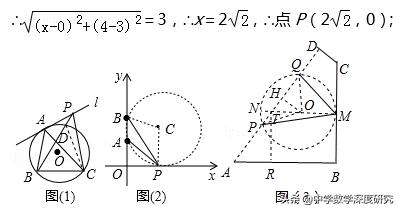
(3)存在.如图(3),过P,Q两点作⊙O与BC相切于点M,过点O作OH⊥AD于H,作直径MN交AD于T,过点T作TR⊥AB于R,连接OP,OQ,设⊙O半径为r,
∵M为BC的中点,∴BM=1/2BC=48(米)
∵MN为⊙O的直径,⊙O与BC相切,TR⊥AB,AB⊥BC
∴∠BMN=∠BRT=∠ABC=90°
∴BMTR是矩形,∴TR=BM=48米,MT=BR,MT∥AB.



