粒子物理学家在20世纪下半叶发展了一个优雅的理论模型,为我们理解宇宙中的基本粒子和力提供了一个框架。这个强大的框架就是所谓的标准模型,它的主要成分之一是希格斯场,这是一种无处不在的量子场,负责赋予粒子质量。由于量子力学中的波粒二象性,希格斯场有一个基本粒子,也就是所谓的希格斯玻色子。
本文的目的是为希格斯玻色子及其性质提供一个更数学的解释。

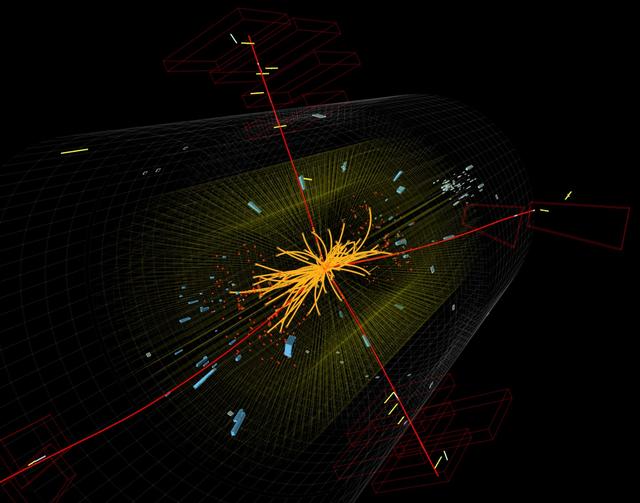
- 图1:这张照片显示了希格斯玻色子衰变成两个光子的事件,绿色的线是它们的能量沉积。这个实验使科学家们能够缩小希格斯粒子的质量范围。
虽然自然的基本法则有几种对称性,但我们的世界远非对称的。用物理学术语来说,拉格朗日函数是对称的,但它们所描述的世界却不是。事实上,研究这种对称性是如何被打破的,是物理学的一个中心主题。
首先,让我们考虑一个对称破缺的例子,其中系统由相互作用的n分量标量场组成。
标量场
考虑一个有分量的n维标量场的拉格朗日量:
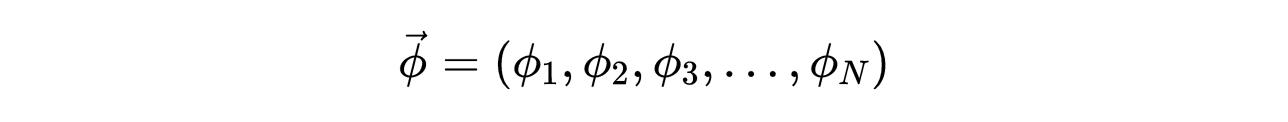
- 式1:n维标量场。
拉格朗日密度为:
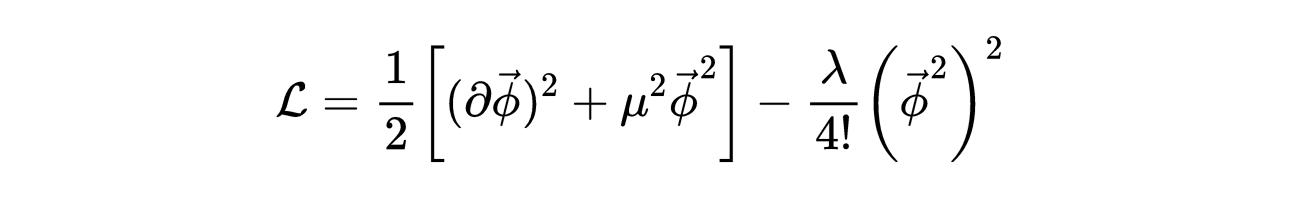
- 式2:旋转对称的拉格朗日密度(N维)。
注意到质量项的符号是负的。拉格朗日函数是:
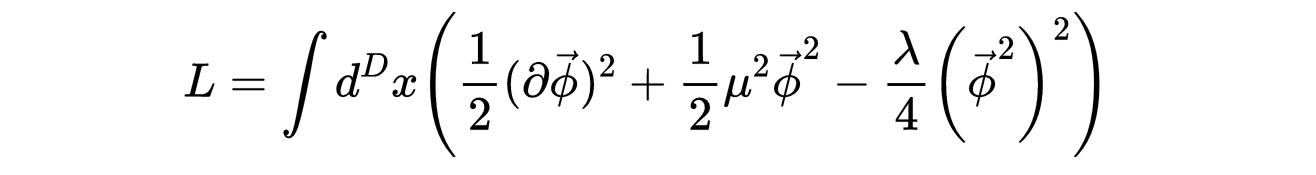
- 式3:拉格朗日量对应的拉格朗日密度。
N = 1情况
如果N=1,拉格朗日函数有极值:
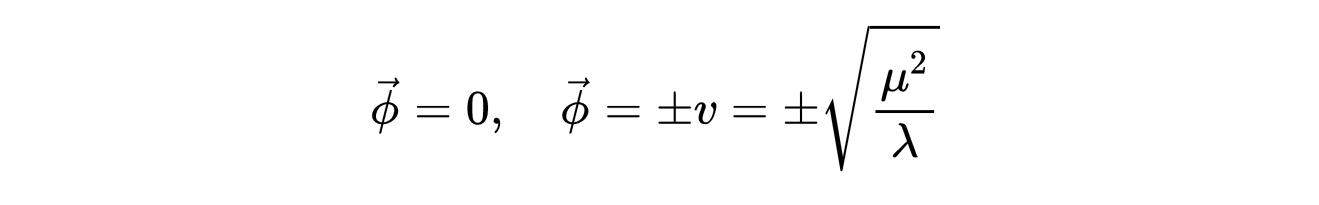
- 式4:拉格朗日系数L的极值。这里,第一个ϕ是局部极大值。
其中ϕ=0为最大值。其它两个ϕ,即v或-v,都是等效的基态,我们可以选择其中之一作为我们的基态。基态称为VEV(真空期望值)。
现在,注意两个极值之间的隧穿势垒是无限的:
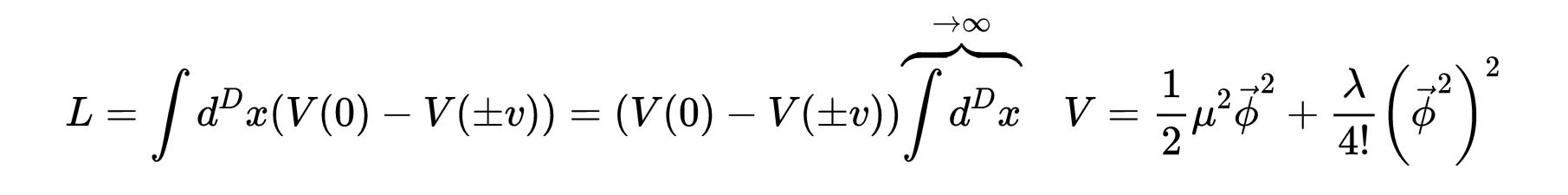
- 式5:在QFT中拉格朗日函数 L的极值之间的势垒是∞
这是因为式5中的时空积分是无限的。由于势垒是无限的,基态波函数(或泛函)不能在极值之间隧穿。因此,普通量子力学中存在的ϕ→-ϕ反射对称性被打破。但是,,对称破坏并不是由于 L中引入新量造成的。
N = 2情况
在这种情况下,势能是著名的墨西哥帽势能。我们现在有无穷多个物理上等价的极小值(或真空)。所有这些真空具有相同的值,即:
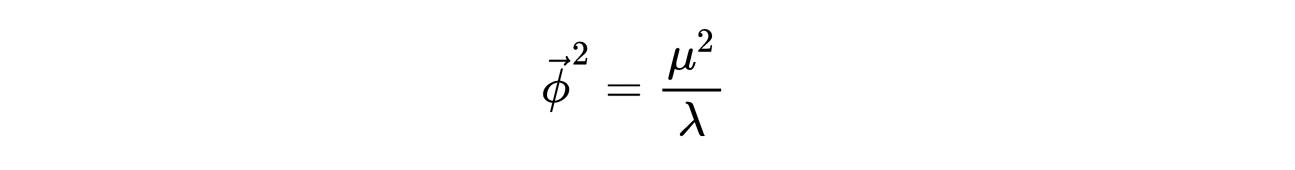
- 式6:N=2时所有最小值的平方。
注意每个最小值点在不同的方向上。但其结果不能依赖于对ϕ方向的选择,因此我将选择:
- ϕ为单向的
- 其中ϕ₁=+v的值由式6给出。
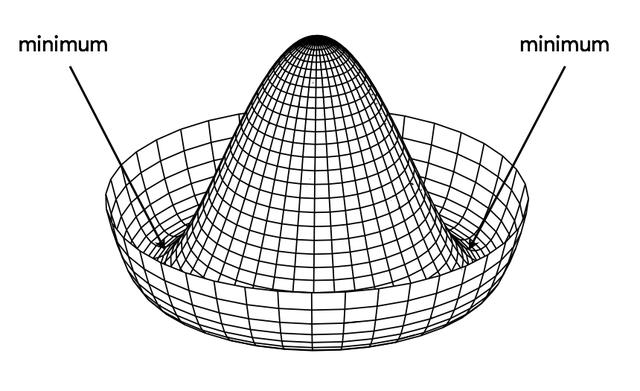
- 图2:“墨西哥帽”势函数V(ϕ)及其无穷极小值
现在我们通过写出极小值来研究ϕ₁和ϕ₂周围的波动:
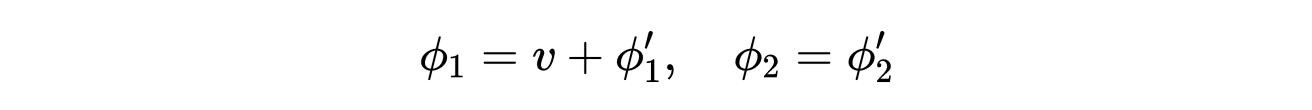
- 式7:在极小值附近的波动。单分量沿径向波动,双分量在电势的最小值处绕圆波动。
将式7代入拉格朗日方程可得:
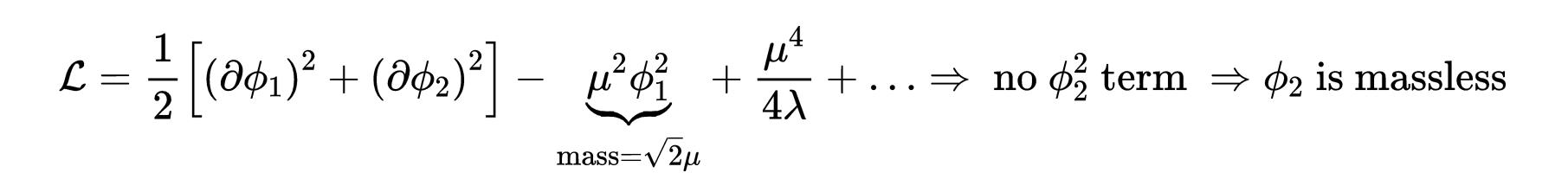
- 式8:ϕ的第二分量是无质量的。
现在我们在拉格朗日方程中加入规范场A。规范理论,根据定义,是一种场论,它的拉格朗日量在某些类型的群的变换下是不变的。根据规范原理,宇宙中三种基本相互作用的基础,如果我们改变描述它的方式,物理性质不应该改变。规范理论有两种类型:阿贝尔理论和非阿贝尔理论。阿贝尔规范理论的一个例子是我们熟悉的电磁理论。
电磁场
我们从电场和磁场E和B的麦克斯韦方程开始:
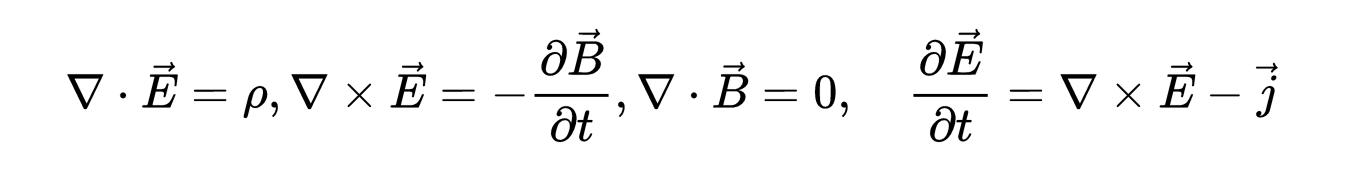
- 式9:麦克斯韦的电场和磁场方程,E和B。
- 图3:描绘了一个地磁暴,其中的带电粒子通量的激增改变了地球的磁场,在大气中诱导电场。
电场和磁场可以用势V和A表示为:
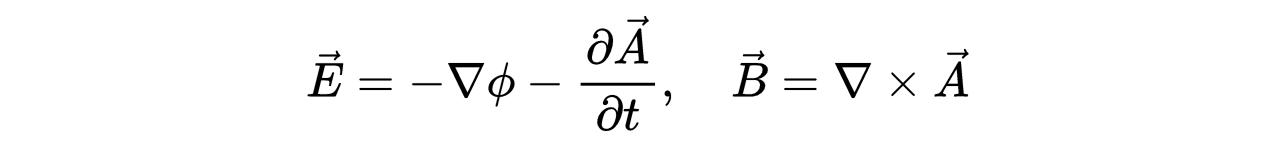
- 式10:用电势V和A表示的电场和磁场。
我们可以把V和A归入向量势:
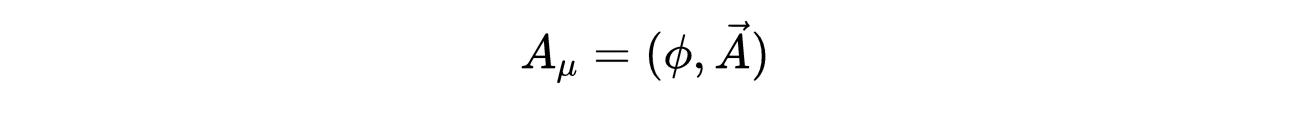
- 式11:对偶向量势
与电磁场有关的拉格朗日,其方程在矢势的规范变换下是不变的:
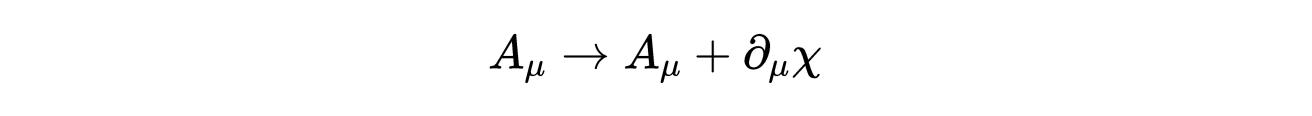
- 式12:一个规范变换,其中χ是一个标量函数
由下式给出:
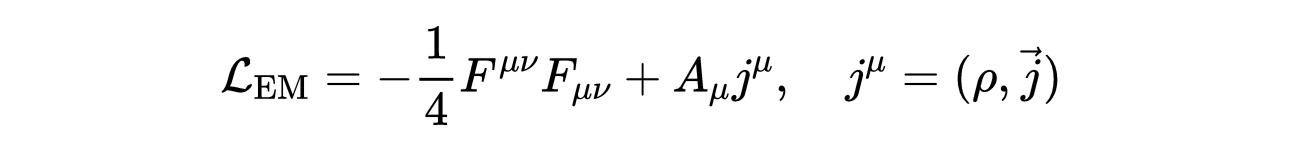
- 式13:电磁场的拉格朗日量。矢量j为以电荷和电流密度为分量的4维电流。
张量F是:
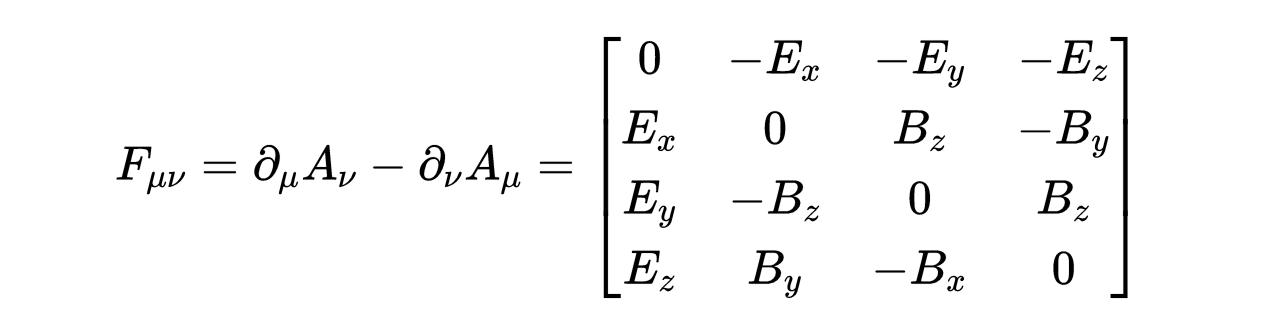
- 式14:电磁场张量。
注意F在规范变换式12下是不变的。阿贝尔规范理论在U(1)群下是全局不变的。n次的酉群U(n)由n × n个酉矩阵组成,采用矩阵乘法的群运算。群U(1)又称圆群,是所有具有模1的复数的乘群。
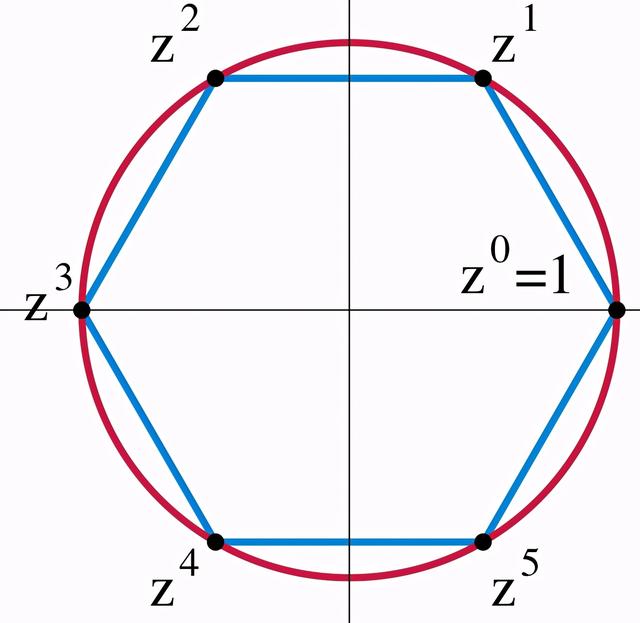
- 图4:圆群U(1)的图示。
狄拉克场ψ是费米子场的一个例子,费米子场是一个量子场,其量子是费米子。这些场服从正则反对易关系,与服从正则对易关系的玻色子场相反。
带电荷e和质量m的狄拉克场具有以下自由拉格朗日量:
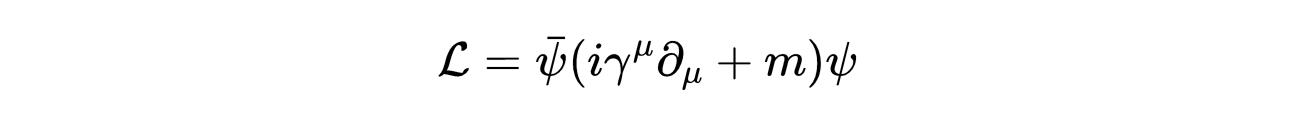
- 式15:自由的狄拉克拉格朗日函数。
这里:
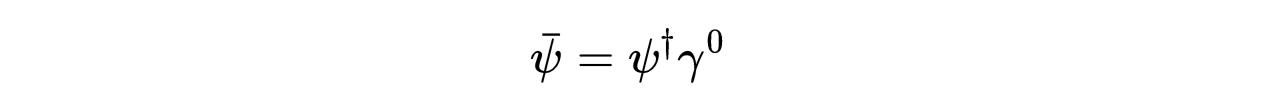

- 式16:狄拉克伴随矩阵。
为狄拉克伴随场,且:
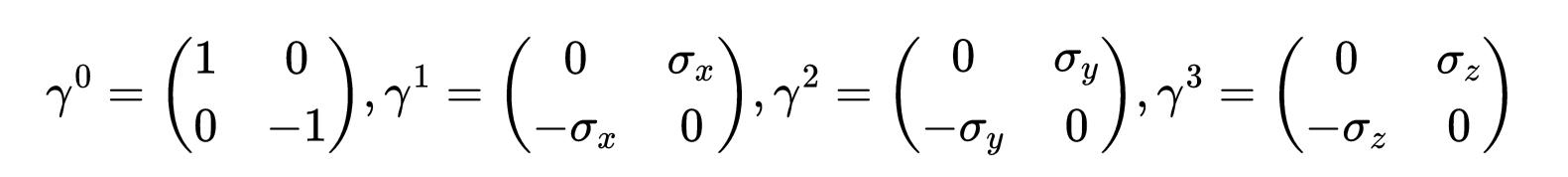
- 式17:γ矩阵的标准表示。
是矩阵的标准表示。狄拉克拉格朗日函数在全局规范变换下是不变的:
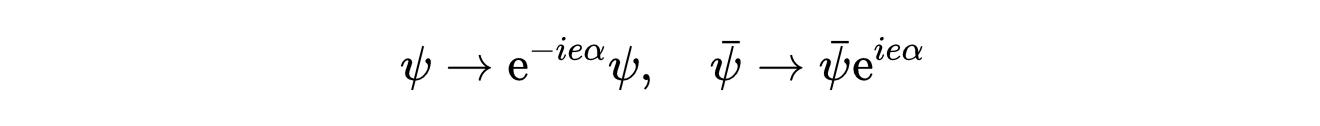
- 式18:全局规范变换。
在局部规范变换中,α成为函数α(x)和新的拉格朗日不变量:
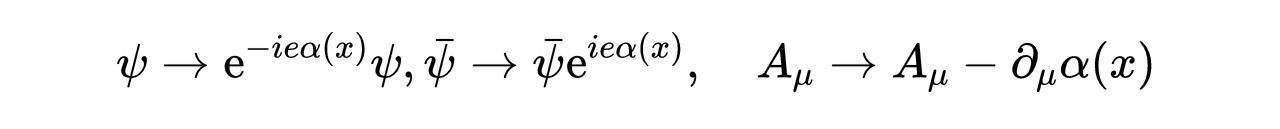
- 式19:局部规范变换。
变成:
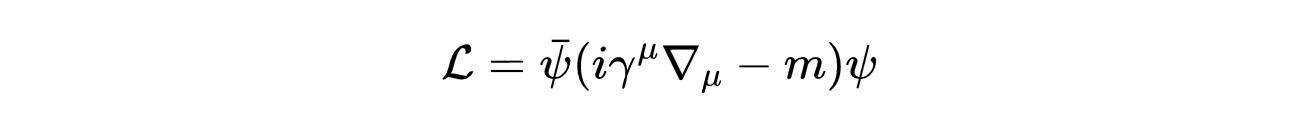
- 式20:局部规范变换下的自由狄拉克拉格朗日不变量。
这里
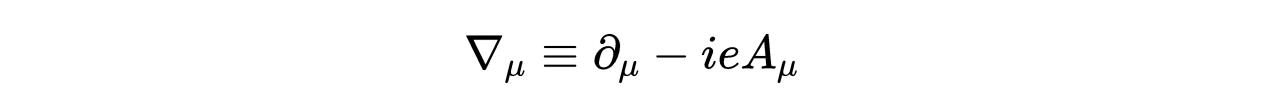
- 式21:协变导数。
包括电磁场和狄拉克场的量子电动力学拉格朗日量是:
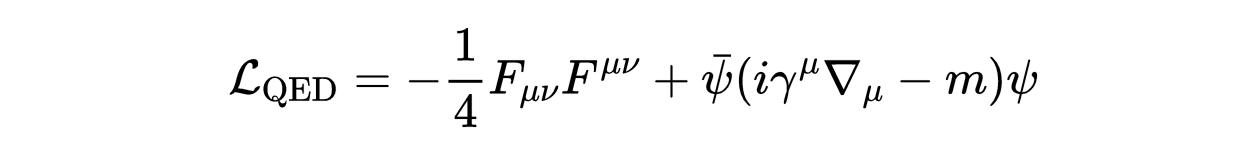
- 式22:量子电动力学(QED)拉格朗日函数。
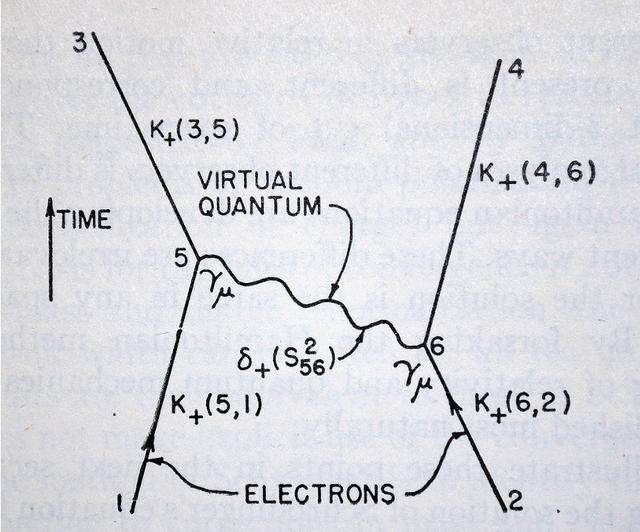
- 图5:第一次发表的费曼图,出现在理查德·费曼的《量子电动力学的时空方法》中
如前所述,我们的世界不是尺度对称的。然而,一个理论有可能具有某种对称性,即使我们对那个物理理论的经验并没有反映出相应的对称性。大量无质量矢量场(如电磁场)的缺失意味着规范对称被打破了。
现在让我们考虑一个在规范理论中如何自发对称破缺的例子。为简单起见,我将考虑最简单的规范理论,即电磁,它是一个U(1)规范场,耦合到其中的一个复标量场。在式18中不变的拉格朗日量为:
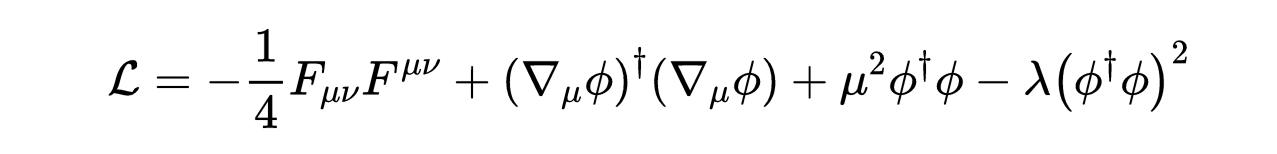
- 式22:耦合于复标量场的U(1)规范场的拉格朗日量。
其中ϕ_1和ϕ_2是ϕ的实部和虚部。
现在我们把标量场写为:

- 式23:极坐标下的标量场。
转换:
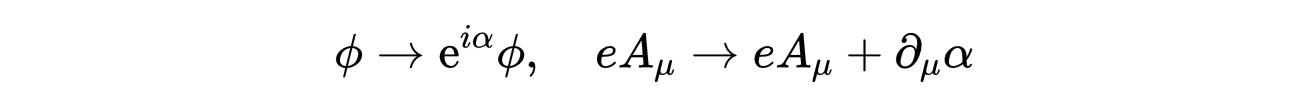
我们生成了一个规范不变组合:
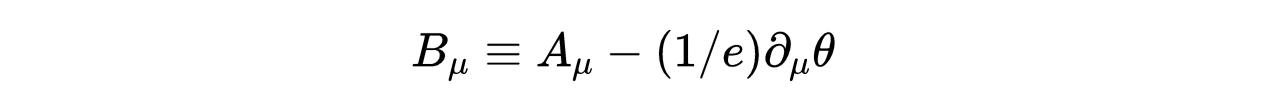
- 式24:规范不变组合。
正如我们之前所做的,我们选择:
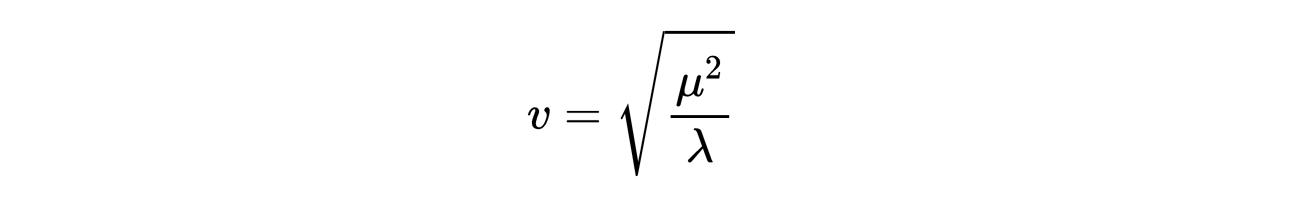
- 式25:标量势最小的点
成为势能最小的值。像之前一样添加一个波动项:
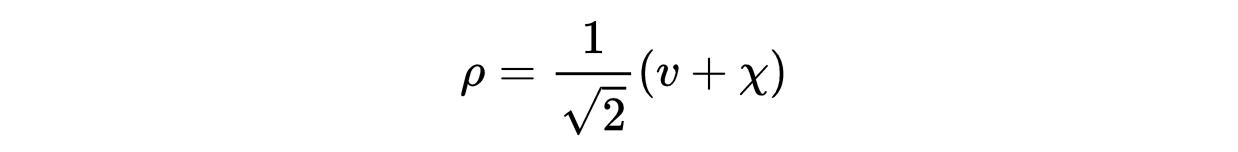
- 为解释自发的对称破缺而增加的涨落项。
我们得到以下拉格朗日量:
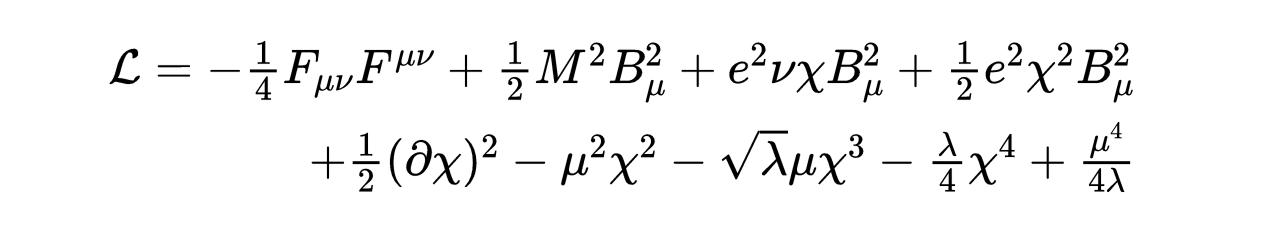
- 式27:拉格朗日公式22增加了一个涨落项来解释自发的对称破缺。
这个拉格朗日定理描述了一个质量为M=ev的向量场B它与标量场χ有质量相互作用
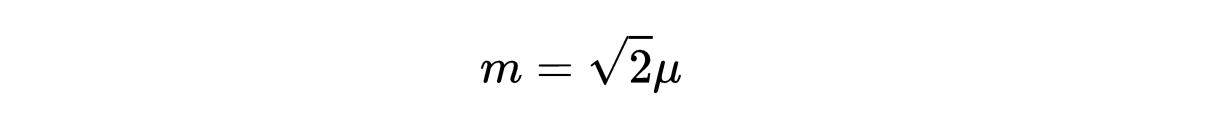
- 式28:标量场的质量χ
注意玻色子θ不在拉格朗日量中。有人说θ被标准场A“吃掉”了,标准场A变成了B。先前的无质量场A有两个自由度,两个极化方向(两个自旋方向)。巨大的规范场获得了一个纵向自由度。从无质量到有质量的这种转变被称为希格斯机制,其中ϕ被称为希格斯场。正如在导论中解释的那样,由于量子力学中的波粒二象性,其中ϕ有一个基本粒子,即所谓的希格斯玻色子。

- 图6:希格斯电势。在底部任意一个点的选择都会自发地破坏旋转U(1)对称。
电弱理论既描述了电磁力,也描述了弱核力。
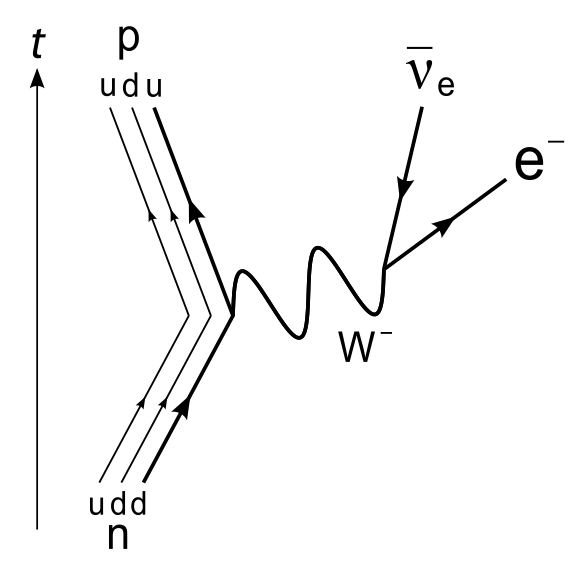
- 图7:中子通过中等重W玻色子衰变为质子、电子和电子反中微子。
这些力看起来非常不同:
- 弱核力的作用距离很小,比原子核还小。
- 电磁力作用于巨大的距离,并与距离的平方成反比。
- 质子间的电磁力比弱核力强10^6倍。
然而,物理学家证明,在所谓的统一能量(~246 GeV)以上,这些力会合并为一个力。
换句话说,超过这个极限阈值,这两种力是一个更基本的电弱力的不同方面。如上所述,无质量规范场A的自发对称性破缺给出了三个质量矢量玻色子的起源,即:
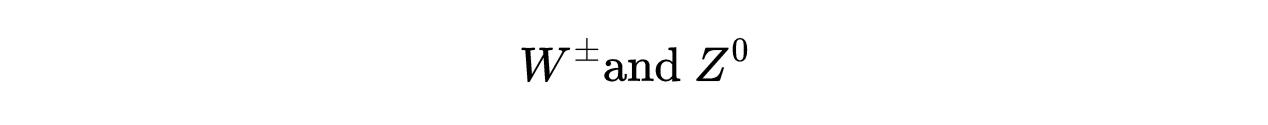
- 式29:一个无质量的规范场A的自发对称性破缺给出了三个大质量玻色子的起源。
换句话说,希格斯机制解释了式29中弱相互作用规范玻色子的质量。
想了解更多精彩内容,快来关注老胡说科学