上接 零基础机器学习入门——浅谈神经网络（四），本节我们主要说说BP算法：

大家可以先简单看看前面的文章，回顾一下前向传播和偏导的概念。本节大家可能会看的比较懵，下一节我们会将这些文字的东西实例化。跳过本节不影响您接下来的学习

BP算法是一种计算偏导数的有效方法，它的基本原理是：利用前向传播最后输出的结果来计算误差的偏导数，再用这个偏导数和前面的隐藏层进行加权求和，如此一层一层地向后传下去，直到输入层(不计算输入层)，最后利用每个节点求出的偏导数来更新权重。

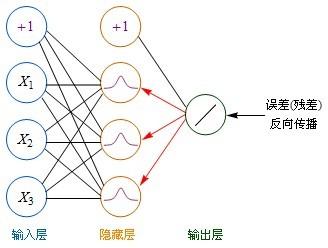
BP反向传播

定义：“残差(error term)”这个词来表示误差的偏导数。

输出层→隐藏层：残差 = -(输出值-样本值) * 激活函数的导数
隐藏层→隐藏层：残差 = (右层每个节点的残差加权求和)* 激活函数的导数
如果输出层用Purelin作激活函数，Purelin的导数是1，输出层→隐藏层：残差 = -(输出值-样本值)
如果用Sigmoid(logsig)作激活函数，那么：Sigmoid导数 = Sigmoid*(1-Sigmoid)
输出层→隐藏层：残差 = -(Sigmoid输出值-样本值) * Sigmoid*(1-Sigmoid) = -(输出值-样本值)*输出值*(1-输出值)
隐藏层→隐藏层：残差 = (右层每个节点的残差加权求和)* 当前节点的Sigmoid*(1-当前节点的Sigmoid)
如果用tansig作激活函数，那么：tansig导数 = 1 - tansig^2

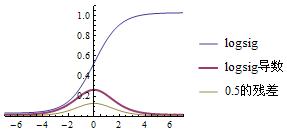
曲线展示

残差全部计算好后，就可以更新权重了：
输入层：权重增加 = 当前节点的Sigmoid * 右层对应节点的残差 * 学习率
隐藏层：权重增加 = 输入值 * 右层对应节点的残差 * 学习率
偏移值的权重增加 = 右层对应节点的残差 * 学习率
学习率前面介绍过，学习率是一个预先设置好的参数，用于控制每次更新的幅度。

此后，对全部数据都反复进行这样的计算，直到输出的误差达到一个很小的值为止。
以上介绍的是目前最常见的神经网络类型，称为前馈神经网络(FeedForward Neural Network)，由于它一般是要向后传递误差的，所以也叫BP神经网络(Back Propagation Neural Network)。

是不是看文字已经兴趣大减？下一节我们就用图形和数字的方式对这些文字进行说明，你会发现原来大名鼎鼎的反向传播算法也不过如此