自变量从x1到x2时,函数值y从f(x1)变化到f(x2),那么函数从x1到x2的平均变化率定义为
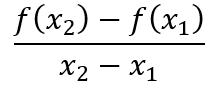
表示变量的增量,更习惯于用下列符号表示
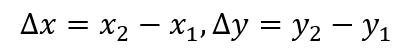
那么函数的平均变化率就可表示为
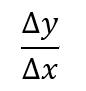
平均变化率表示的是函数值随自变量在一个区间范围内变化的平均值,平均变化率越大表示函数值的平均变化越快。为了更容易理解其含义,举个物理上的例子:位移在一段时间内的平均变化率就是平均速度。
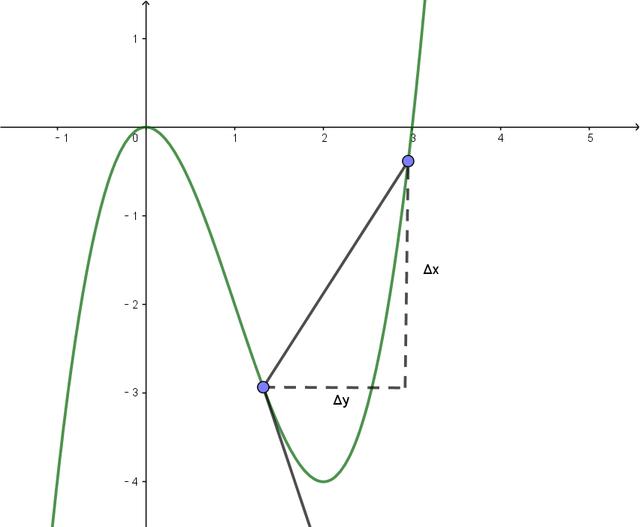

当自变量的增量逐渐减小并趋于0时,平均变化率就变成了瞬时变化率可用下列表达式表示
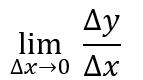
函数在某个自变量取值处存在瞬时变化率的前提是,函数值在此处必须为连续变化的。瞬时变化率表示的是,函数值在某点处的变化趋势。
瞬时变化率其实就是导数,变化率和导数是研究函数图像走势的基础概念,是非常有用的工具,应该理解并牢记其定义。
本文由小朱与数学原创,欢迎关注,带你一起长知识!