并查集的概念

在计算机科学中，并查集（英文：Disjoint-set data structure，直译为不交集数据结构）是一种数据结构，用于处理一些不交集（Disjoint sets，一系列没有重复元素的集合）的合并及查询问题。并查集支持如下操作：

- 查询：查询某个元素属于哪个集合，通常是返回集合内的一个“代表元素”。这个操作是为了判断两个元素是否在同一个集合之中。

- 合并：将两个集合合并为一个。

- 添加：添加一个新集合，其中有一个新元素。添加操作不如查询和合并操作重要，常常被忽略。

理解下面三句话，并查集就学会了：

“并”的意思是把两个处在同一个连通分量的结点给并到一起.

“查”的意思是查找一个结点的根节点.

“并”的时候需要用到“查”

不过这样还是比较晦涩。下面我们用图片的方式来讲讲。

图解并查集

并查集的重要思想在于，用集合中的一个元素代表集合。

刚开始好比诸侯国，各自为政。

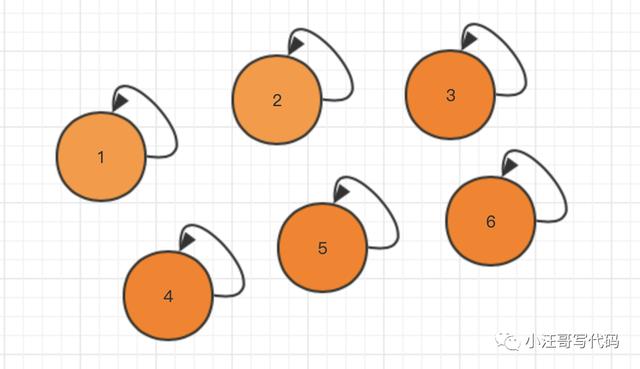
后来3号被1号吞并了，定都1号城池。

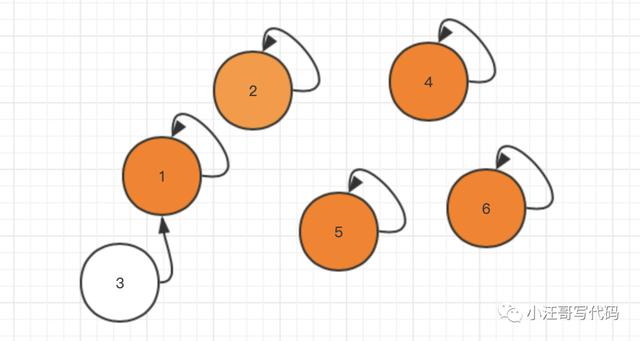
同时2号也被1号吞并了，定都1号城池。

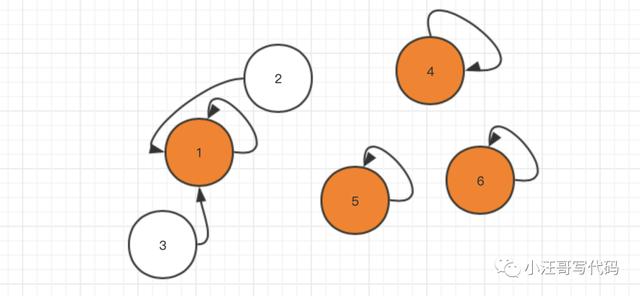
神州大地上 4，5，6也发生着相同的事情，5，6也背4号诸侯吞并了，定都4号城池。

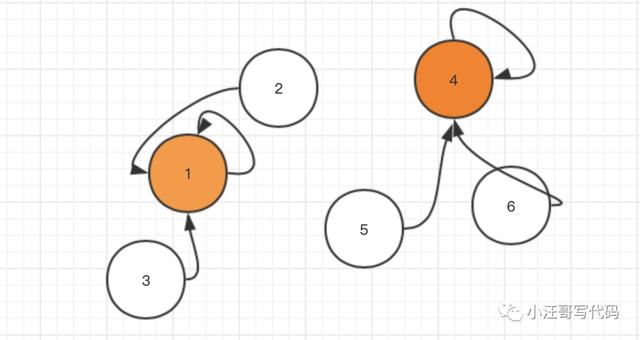
后来1号把4号给吞并了，5，6也连带成了1号的领土。定都1号城池。

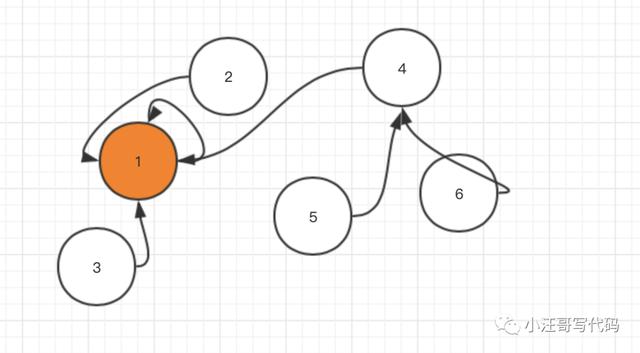
学习过前面的二叉树，其实我们可以把并查集想象成一个数的结构。

要寻找集合的代表元素（都城），只需要一层一层往上访问父节点（图中箭头所指的圆），直达树的根节点（图中橙色的圆）即可。

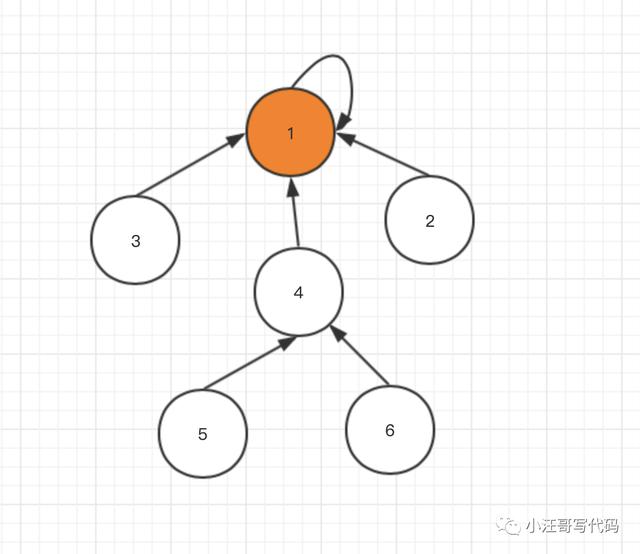
并查集实现代码

public static class Node<V> { V value; public Node(V v) { value = v; } } public static class UnionFind<V> { public HashMap<V, Node<V>> nodes;//所有的节点 public HashMap<Node<V>, Node<V>> parents;// 每个节点的父几点 public HashMap<Node<V>, Integer> sizeMap;// 每个父节点有多少个孩子 public UnionFind(List<V> values) { nodes = new HashMap<>(); parents = new HashMap<>(); sizeMap = new HashMap<>(); for (V cur : values) { Node<V> node = new Node<>(cur); nodes.put(cur, node); parents.put(node, node); sizeMap.put(node, 1); } } // 给你一个节点，请你往上到不能再往上，把代表返回 public Node<V> findFather(Node<V> cur) { Stack<Node<V>> path = new Stack<>(); while (cur != parents.get(cur)) { path.push(cur); cur = parents.get(cur); } while (!path.isEmpty()) { //优化 parents.put(path.pop(), cur); } return cur; } //两个节点是不是在同一集合里 public boolean isSameSet(V a, V b) { return findFather(nodes.get(a)) == findFather(nodes.get(b)); } //合并两个节点 public void union(V a, V b) { Node<V> aHead = findFather(nodes.get(a)); Node<V> bHead = findFather(nodes.get(b)); if (aHead != bHead) { int aSetSize = sizeMap.get(aHead); int bSetSize = sizeMap.get(bHead); Node<V> big = aSetSize >= bSetSize ? aHead : bHead; Node<V> small = big == aHead ? bHead : aHead; //把数量少的节点挂在数据多的节点下面，可以避免路径过长 parents.put(small, big); sizeMap.put(big, aSetSize + bSetSize); sizeMap.remove(small); } } public int sets() { return sizeMap.size(); } }

应用场景

leetcode朋友圈问题

https://leetcode.com/problems/friend-circles/

上面的并查集是HashMap用实现，常数时间比较长。下面我们用数组实现。数组直接寻址，速度比较快。

public static int findCircleNum(int[][] M) { int N = M.length; // {0} {1} {2} {N-1} UnionFind unionFind = new UnionFind(N); for (int i = 0; i < N; i++) { for (int j = i + 1; j < N; j++) { if (M[i][j] == 1) { // i和j互相认识 unionFind.union(i, j); } } } return unionFind.sets(); } public static class UnionFind { // parent[i] = k ：i的父亲是k private int[] parent; // size[i] = k ：如果i是代表节点，size[i]才有意义，否则无意义 // i所在的集合大小是多少 private int[] size; // 辅助结构 private int[] help; // 一共有多少个集合 private int sets; public UnionFind(int N) { parent = new int[N]; size = new int[N]; help = new int[N]; sets = N; for (int i = 0; i < N; i++) { parent[i] = i; size[i] = 1; } } // 从i开始一直往上，往上到不能再往上，代表节点，返回 // 这个过程要做路径压缩 private int find(int i) { int hi = 0; while (i != parent[i]) { help[hi++] = i; i = parent[i]; } for (hi--; hi >= 0; hi--) { parent[help[hi]] = i; } return i; } public void union(int i, int j) { int f1 = find(i); int f2 = find(j); if (f1 != f2) { if (size[f1] >= size[f2]) { size[f1] += size[f2]; parent[f2] = f1; } else { size[f2] += size[f1]; parent[f1] = f2; } sets--; } } public int sets() { return sets; } }

leetcode岛屿问题

https://leetcode.com/problems/number-of-islands/

1.感染法

public static int numIslands(char[][] board) { int islands = 0; for (int i = 0; i < board.length; i++) { for (int j = 0; j < board[0].length; j++) { if (board[i][j] == '1') { islands++; infect(board, i, j); } } } return islands; } // 从(i,j)这个位置出发，把所有练成一片的'1'字符，变成0 public static void infect(char[][] board, int i, int j) { if (i < 0 || i == board.length || j < 0 || j == board[0].length || board[i][j] != '1') { return; } board[i][j] = 0; infect(board, i - 1, j); infect(board, i + 1, j); infect(board, i, j - 1); infect(board, i, j + 1); }

2.并查集-hashmap

public static int numIslands1(char[][] board) { int row = board.length; int col = board[0].length; Dot[][] dots = new Dot[row][col]; List<Dot> dotList = new ArrayList<>(); for (int i = 0; i < row; i++) { for (int j = 0; j < col; j++) { if (board[i][j] == '1') { dots[i][j] = new Dot(); dotList.add(dots[i][j]); } } } UnionFind1<Dot> uf = new UnionFind1<>(dotList); for (int j = 1; j < col; j++) { // (0,j) (0,0)跳过了 (0,1) (0,2) (0,3) if (board[0][j - 1] == '1' && board[0][j] == '1') { uf.union(dots[0][j - 1], dots[0][j]); } } for (int i = 1; i < row; i++) { if (board[i - 1][0] == '1' && board[i][0] == '1') { uf.union(dots[i - 1][0], dots[i][0]); } } for (int i = 1; i < row; i++) { for (int j = 1; j < col; j++) { if (board[i][j] == '1') { if (board[i][j - 1] == '1') { uf.union(dots[i][j - 1], dots[i][j]); } if (board[i - 1][j] == '1') { uf.union(dots[i - 1][j], dots[i][j]); } } } } return uf.sets(); } public static class Dot { //这里只是用了dot的内存地址 } public static class Node<V> { V value; public Node(V v) { value = v; } } public static class UnionFind1<V> { public HashMap<V, Node<V>> nodes; public HashMap<Node<V>, Node<V>> parents; public HashMap<Node<V>, Integer> sizeMap; public UnionFind1(List<V> values) { nodes = new HashMap<>(); parents = new HashMap<>(); sizeMap = new HashMap<>(); for (V cur : values) { Node<V> node = new Node<>(cur); nodes.put(cur, node); parents.put(node, node); sizeMap.put(node, 1); } } public Node<V> findFather(Node<V> cur) { Stack<Node<V>> path = new Stack<>(); while (cur != parents.get(cur)) { path.push(cur); cur = parents.get(cur); } while (!path.isEmpty()) { parents.put(path.pop(), cur); } return cur; } public void union(V a, V b) { Node<V> aHead = findFather(nodes.get(a)); Node<V> bHead = findFather(nodes.get(b)); if (aHead != bHead) { int aSetSize = sizeMap.get(aHead); int bSetSize = sizeMap.get(bHead); Node<V> big = aSetSize >= bSetSize ? aHead : bHead; Node<V> small = big == aHead ? bHead : aHead; parents.put(small, big); sizeMap.put(big, aSetSize + bSetSize); sizeMap.remove(small); } } public int sets() { return sizeMap.size(); } }

3.并查集-数组

public static int numIslands2(char[][] board) { int row = board.length; int col = board[0].length; UnionFind2 uf = new UnionFind2(board); for (int j = 1; j < col; j++) { if (board[0][j - 1] == '1' && board[0][j] == '1') { uf.union(0, j - 1, 0, j); } } for (int i = 1; i < row; i++) { if (board[i - 1][0] == '1' && board[i][0] == '1') { uf.union(i - 1, 0, i, 0); } } for (int i = 1; i < row; i++) { for (int j = 1; j < col; j++) { if (board[i][j] == '1') { if (board[i][j - 1] == '1') { uf.union(i, j - 1, i, j); } if (board[i - 1][j] == '1') { uf.union(i - 1, j, i, j); } } } } return uf.sets(); } public static class UnionFind2 { private int[] parent; private int[] size; private int[] help; private int col; private int sets; public UnionFind2(char[][] board) { col = board[0].length; sets = 0; int row = board.length; int len = row * col; parent = new int[len]; size = new int[len]; help = new int[len]; for (int r = 0; r < row; r++) { for (int c = 0; c < col; c++) { if (board[r][c] == '1') { int i = index(r, c); parent[i] = i; size[i] = 1; sets++; } } } } // (r,c) -> i private int index(int r, int c) { return r * col + c; } // 原始位置 -> 下标 private int find(int i) { int hi = 0; while (i != parent[i]) { help[hi++] = i; i = parent[i]; } for (hi--; hi >= 0; hi--) { parent[help[hi]] = i; } return i; } public void union(int r1, int c1, int r2, int c2) { int i1 = index(r1, c1); int i2 = index(r2, c2); int f1 = find(i1); int f2 = find(i2); if (f1 != f2) { if (size[f1] >= size[f2]) { size[f1] += size[f2]; parent[f2] = f1; } else { size[f2] += size[f1]; parent[f1] = f2; } sets--; } } public int sets() { return sets; } }

leetcode岛屿问题二

https://leetcode.com/problems/number-of-islands-ii/

public static List<Integer> numIslands(int m, int n, int[][] positions) { UnionFind1 uf = new UnionFind1(m, n); List<Integer> ans = new ArrayList<>(); for (int[] position : positions) { ans.add(uf.connect(position[0], position[1])); } return ans; } public static class UnionFind1 { private int[] parent; private int[] size; private int[] help; private final int row; private final int col; private int sets; public UnionFind1(int m, int n) { row = m; col = n; sets = 0; int len = row * col; parent = new int[len]; size = new int[len]; help = new int[len]; } private int index(int r, int c) { return r * col + c; } private int find(int i) { int hi = 0; while (i != parent[i]) { help[hi++] = i; i = parent[i]; } for (hi--; hi >= 0; hi--) { parent[help[hi]] = i; } return i; } private void union(int r1, int c1, int r2, int c2) { if (r1 < 0 || r1 == row || r2 < 0 || r2 == row || c1 < 0 || c1 == col || c2 < 0 || c2 == col) { return; } int i1 = index(r1, c1); int i2 = index(r2, c2); if (size[i1] == 0 || size[i2] == 0) { return; } int f1 = find(i1); int f2 = find(i2); if (f1 != f2) { if (size[f1] >= size[f2]) { size[f1] += size[f2]; parent[f2] = f1; } else { size[f2] += size[f1]; parent[f1] = f2; } sets--; } } public int connect(int r, int c) { int index = index(r, c); if (size[index] == 0) { parent[index] = index; size[index] = 1; sets++; union(r - 1, c, r, c); union(r + 1, c, r, c); union(r, c - 1, r, c); union(r, c + 1, r, c); } return sets; } }